Os determinantes são objetos matemáticos muito importantes para diversas áreas, sobretudo para a álgebra linear. Com efeito, esses objetos são capazes de fornecer números reais e/ou complexos a partir de matrizes quadradas. Ademais, a determinação desses valores pode ter influencia direta em diversas áreas e ainda pode ser útil para a determinação de
- equações de lugares geométricos (retas e planos),
- Áreas e volumes,
- Vetores e rotacionais de vetores ortogonais,
- Existência de soluções em sistemas lineares,
- Dependência e independência linear de vetores,
- Dependência de soluções em equações diferenciais.
Nesse sentido, segue que os determinantes são amplamente significativos para o estudo de diversos campos da matemática. Portanto, é extremamente necessário que você gurunauta domine as técnicas para calcula determinantes. Assim, nesse artigo vamos trazer um resumo especificado sobre esse assunto e o passo a passo de como calcular determinantes de forma geral. Então, vem conosco gurunauta que hoje teremos um mega tutorial para você!.
A história dos determinantes
A história dos determinantes remonta ao século XVIII, quando matemáticos começaram a explorar e desenvolver conceitos relacionados à álgebra linear. Com efeito, no século XVIII, matemáticos pioneiros começaram a explorar a álgebra linear e desenvolveram conceitos que abririam caminho para os determinantes. Nesse sentido, um desses matemáticos que ganha notáveis destaques é o suíço Gabriel Cramer, que em 1750 introduziu o conceito de “coeficientes determinantes” em seu livro intitulado “Introdução ao Estudo do Álgebra Linear”. Ademais, Cramer percebeu que esses coeficientes poderiam ser usados para encontrar soluções de sistemas de equações lineares. No entanto, ele não avançou muito além disso em sua pesquisa.
Entretanto, foi somente no final do século XVIII e início do século XIX que outros matemáticos notáveis, como Carl Friedrich Gauss e Augustin-Louis Cauchy, começaram a explorar mais profundamente os determinantes. Com efeito, Gauss, um dos maiores matemáticos de todos os tempos, desenvolveu métodos para resolver sistemas de equações lineares usando o conceito de determinantes. Além disso, ele também estabeleceu as bases para a teoria desses objetos, mostrando sua relação com a inversibilidade de matrizes.
Ademais, outro grande matemático que fez contribuições significativas para essa teoria foi Augustin-Louis Cauchy. Decerto, foi Cauchy que estabeleceu diversas propriedades importantes desses objetos como a multiplicatividade e a relação com a transposta de uma matriz. Além disso, outro grande matemático a ser considerado aqui é Cayley o qual realizou a formalização da descrição moderna dos determinantes alem de introduzir a noção de matriz adjunta.
Por fim, no século XX, os determinantes se tornaram uma ferramenta essencial na álgebra linear e em muitos outros campos da matemática. Em suma, hoje eles são amplamente utilizados em áreas como análise de sistemas lineares, transformações lineares, teoria das matrizes, geometria e física teórica.
Aplicações dos determinantes
Hoje em dia, os determinantes são estudados em cursos de matemática em todo o mundo e desempenham um papel fundamental em diversas aplicações práticas. Ademais, eles possuem várias aplicações em diferentes áreas da matemática e além. Com efeito, algumas das principais aplicações dos determinantes incluem:
- Solução de sistemas de equações lineares. Eles podem determinar se um sistema de equações lineares tem uma solução única, infinitas soluções ou nenhuma solução e também determinar soluções caso o sistema tenha solução.
- Inversão de matrize. Eles podem para determinar se uma matriz é inversível. Se o determinante de uma matriz for diferente de zero, então a matriz é inversível e sua inversa segue do uso do determinante.
- Área e volume: Em geometria, os determinantes podem ser usados para calcular a área de um paralelogramo ou o volume de um paralelepípedo com base nos vetores que o definem.
- Transformações lineares: Os determinantes são usados para determinar se uma transformação linear preserva a orientação dos vetores. Se o determinante da matriz que representa a transformação for diferente de zero, então a transformação preserva a orientação.
- Teoria dos valores próprios. Os determinantes desempenham um papel fundamental na teoria dos valores próprios, que estuda as propriedades dos valores próprios e vetores próprios de uma matriz.
- Física e engenharia: Os determinantes são amplamente utilizados em várias aplicações na física e engenharia, como mecânica clássica, eletromagnetismo, mecânica dos fluidos e teoria dos circuitos. Eles podem ser usados para resolver problemas envolvendo forças, momentos, campos elétricos e magnéticos, entre outros.
Cálculo prático de determinantes
Agora, vamos nos ater a calcular determinantes de forma prática e direta. Com efeito, nós vamos conseguir obter relações simples e faremos alguns exemplos que ilustram bem grande parte dessa teoria. Assim, vamos seguir uma noção de atacar o problema de forma prática, assim, aqui vamos nos focar nas formas gerais para a determinação dos determinantes. Ou seja, não abordaremos todos os métodos possíveis e existentes que permitem esse cálculo, na verdade, vamos atacar o problema para os casos das matrizes 2×2 e os métodos de Sarrus e Laplace. Com efeito, esses dois métodos sãos alternativas extremamente consistentes para o cálculo desejado e logo serão mais do que necessárias para que você consiga dominar completamente esse assunto.
Determinantes de matrizes 2×2
Então, vamos de início começar com o caso particular 2×2. Com efeito, sabemos que nossos determinantes são associados a matrizes quadradas. Portanto, segue que a matriz de menor ordem possível que podemos ter é a matriz de ordem 2. Em suma, as matrizes de ordem 2 são simples e diretas de serem calculadas, na verdade, precisamos apenas de duas multiplicações para tanto.
Então, o determinante D de uma matriz 2×2 pode ser posto como a subtração entre o produto dos elementos da diagonal principal e da diagonal secundária. Com efeito, vamos ser mais ilustrativos e calcularemos o determinante da seguinte matriz

Decerto, o seu cálculo é direto e basta fazermos o indicado como segue passo a passo a seguir:

Assim, apenas com isso já temos o desejado. Ademais, vale aqui ressaltar um ponto muito importante que é o fato de que esse método serve apenas para matrizes 2×2. Portanto, nos casos de matrizes de ordens superiores será necessário empregarmos métodos específicos como o método de Sarrus e/ou Laplace.
Método de Sarrus
Agora, vamos ver o famoso método de Sarrus. Em suma, esse método é o mais prático e universal de todos, não apenas isso mas ele é um método simples de ser empregado por qualquer pessoa uma vez que não requer quaisquer passagens mirabolantes.
Tendo em isso vista, vamos o cálculo do determinante via método de sarrus para o caso 3×3 o qual prosseguimos repetindo as duas primeiras colunas após o determinante e fazemos as multiplicações seguindo as setas indicadas. Além disso, as linhas em direção à esquerda devem multiplicar ainda por -1. Logo, teremos o seguinte.

Assim, podemos fazer o seguinte exemplo.

Todavia, vale ressaltar que a medida que aumentamos a ordem da matriz será necessário colocarmos mais 1 coluna após o determinante. Tome cuidado gurunauta!, isso já me custou uma boa questão em uma prova.
Método de Laplace
O método de Laplace é formal e mais rigoroso. Além disso, esse método é útil em cálculos de determinantes de ordem 3 uma vez que reduz a ordem a problemas do cálculo de determinantes de ordem 2. Nesse sentido, veja que para a mesma matriz do exemplo acima nós teremos que

aqui escolhemos a primeira linha como referencia para o cálculo. Agora, vamos então prosseguir com o cálculo para o determinante. Com efeito, veja que teremos o seguinte.
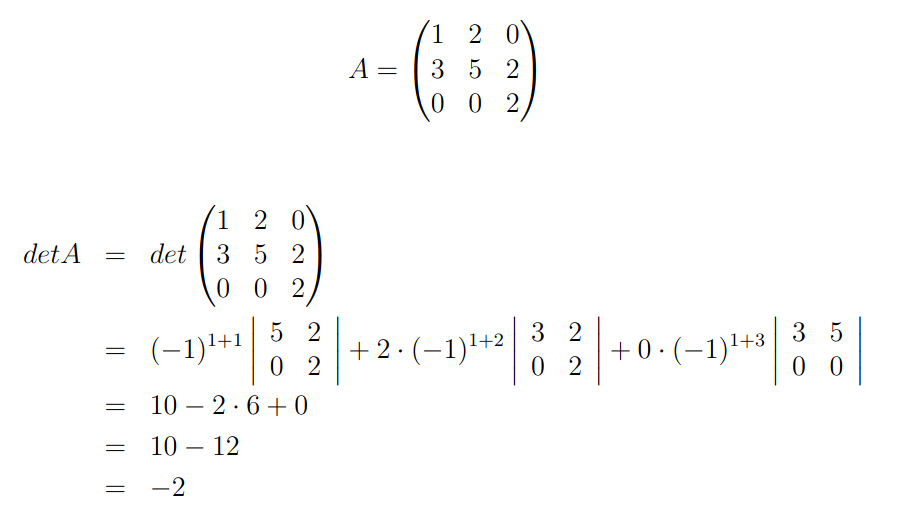
Com efeito, você pode ver que por diferentes métodos o cálculo do determinante resultou no mesmo valor assim assegurando a consistência nos cálculos.
Referências
- WEINTRAUB, Steven H. Determinantes: uma perspectiva histórica. Revista Brasileira de Ensino de Matemática, v. 34, n. 1, p. 157-184, 2012.
- BRUALDI, Richard A. Determinantes: uma revisão. Matemática Contemporânea, v. 45, n. 2, p. 87-110, 2019.
- EIDERMAN, V. Ya. Determinantes e suas aplicações na física matemática. Journal of Mathematical Physics, v. 28, n. 3, p. 589-601, 1999.
- VEIN, Robert. Determinantes e seus usos na física matemática. International Journal of Theoretical Physics, v. 42, n. 6, p. 1203-1227, 2003.
- KRISHNAIAH, Paruchuri R. Determinantes e suas aplicações em estatística. Journal of Statistical Planning and Inference, v. 145, n. 2, p. 295-307, 2015.
- LAY, David C. Álgebra Linear e Suas Aplicações. 5. ed. Rio de Janeiro: LTC, 2015.
- MEYER, Carl D. Análise de Matrizes e Álgebra Linear Aplicada. 2. ed. São Paulo: LTC, 2012.
- AXLER, Sheldon. Álgebra Linear Feita Certa. Rio de Janeiro: Bookman, 2018.
- GOLUB, Gene H.; VAN LOAN, Charles F. Computações Matriciais. 4. ed. São Paulo: Editora Unicamp, 2013.
- MATEMATICANDO. Álgebra Linear: conceitos e aplicações. Matematicando, [S.l.], [s.d.]. Disponível em: https://www.matematicando.net.br/algebra-linear-conceitos-e-aplicacoes/. Acesso em: 22 Set. 2023.
- STRANG, Gilbert. Introdução à Álgebra Linear. 3. ed. São Paulo: Cengage Learning, 2019.





