Regra de três composta na prática com exercícios

Regra de três composta é um dos assuntos que compõem a gama de tópicos da matemática básica. Certamente, construir uma forte base em matemática é fundamental para que você consiga progredir seus estudos em matemática para além dos assuntos basilares indo até níveis mais altos. Assim, domminar a matemática básica de forma sólida e consistente é de fundamental importância, logo, tópicos como funções, trigonometria, geometria plana, geometria espacial, geometria euclidiana, razões e proporcionais são destaques nesses contexto.

Tendo isso em vista, nós da MeuGuru desenvolvemos esse texto focado em te dar um material sobre um desses assuntos: as regras de três compostas. Com efeito, esse artigo está como mais um da série de artigos envolvendo matemática básica aqui do blog da MeuGuru e, nesse texto exploraremos o caso de razões e proporções para além das regras de três simples. Então, vem com a gente que hoje iremos explorar as regras de três compostas tanto em teoria como na prática com a solução de exercícios feitos passo a passo.

Razões e proporções

Então, para começarmos nosso texto é importante revisitarmos, brevemente, as noções em volta de razões e proporções. Com efeito, razões e proporções aparecem na matemática com intuito de estabelecer comparações efetivas entre grandezas distintas que, por algum fator, podem estar relacionadas. Nesse sentido, vale mencionarmos, por exemplo, o caso de uma receita de bolo, na qual temos um manual de instruções para prepararmos o bolo, entretanto, o que chama atenção aqui são as relações dos ingredientes, para um bolo de chocolate temos, tradicionalmente o seguinte.

• 4 ovos
• 4 colheres (sopa) de chocolate em pó
• colheres (sopa) de manteiga
• 3 xícaras (chá) de farinha de trigo
• 2 xícaras (chá) de açúcar
• 2 colheres (sopa) de fermento
• 1 xícara (chá) de leite

Certamente, se perguntarmos para uma pessoa se é possível fazer tal receita com apenas 2 ovos ela irá questionar você sobre suas habilidades culinárias e dirá que até será possível mas o bolo não terá um bom resultado. De fato, isso ocorre em virtude de uma relação de proporção, a qual é estabelecida entre todos os ingredientes e a possibilidade fazer exatamente 1 bolo. Portanto, podemos dizer que há uma razão entre ingredientes e bolos 4 ovos estão para 1 bolo, ou que 8 cholheres de sopa de chocolate em pó estão para dois bolo se analisarmos cada ingrediente individualmente.

Proporções em matemática: Matematizando as coisas

Perceba que o exemplo da receita não só introduz a nós a noção de proporcionalidade como também de razão e essas são estabelecidas para mais de uma quantidade. Por conseguinte, isso é de extremo interesse para nosso artigo pois essa é a base para estabelecermos a noção que permeia as regras de três compostas, visto que essas razões estabelecem-se para quanto temos mais de duas quantidades envolvidas.

Mas afinal, o que significa dizer que quantidades estão em razão ou que são proporcionais?. Em suma, denotamos que uma quantidade A é proporcional a uma quantidade B por:

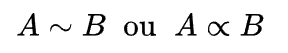
Ademais, dizer que A é proporcional a B é implica ainda dizer que existe um termo k que é uma constante de proporcionalidade entre A e B que é tal que A e B podem ser escritos como.

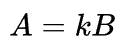
Assim, as noções matemáticas acerca de proporções são estabelecidas quanto a sua notação e definição. Não só isso, vale ainda lembrar que tais constantes de proporcionalidades podem desempenhar papeis extremamente significativos para certos contextos. A citar, temos a física a qual, em várias áreas como gravitação newtoniana e mesmo na eletricidade percebemos a presença de constantes que foram determinadas visto que um padrão de proporcionalidade na natureza foi descoberto. Assim, vemos que a constante da gravitação universal G = 6.67 10^-11 Nm²/Kg² e a constante eletrostática do vácuo K = 9.10⁹ N.m² /C² são exemplos disso, uma vez que ao percerber a relação de proporção direta entre força gravitacional (eletrostática) e massa (carga elétrica) tornou-se possível calcular tais constantes.

Regra de três composta – Conhecendo a teoria

Então, agora que temos em mente o que são proporções e razões podemos avançar para a teoria que permeia o assunto principal desse artigo. Em suma, já abordamos aqui em nosso blog um texto específico sobre regra de três simples e agora devemos avançar para o caso composto. Esse caso consiste, simplesmente, em avaliarmos problemas com mais de uma grandeza em proporção.

Bom, isso é na verdade é algo fácil de aprender e nós da MeuGuru vamos te mostrar como você pode fazer isso. Para tanto, é imprescindível que você tenha entendido a existência de uma constante entre grandezas proporcionais. Uma vez que, para tratarmos problemas com proporcionalidade no caso composto é imprescindível que usemos essa abordagem. Na seção seguinte te mostraremos como resolver um problema desse tipo na prática com passo a passo e discussão sobre o assunto.

Exercício resolvido sobre regra de três composta

Então, comecemos com o problema de três grandezas A, B e C que vamos contextualizá-las, para facilitar o entendimento da seguinte forma

• A grandeza A é o tempo de execução de uma determinada obra,
• A grandeza B é a quantidade de construtores que farão essa obra,
• Já C representa a quantidade de avanços da obra para B pedreiros.

Analisando proporcionalidades em regra de três composta

Um clássico exemplo nesse contexto é a construção de um muro, o qual sabemos que se tivermos 10 construtores, esses 10 constrõem o 7 metros de muro em um tempo de 3 dias. Com isso, podemos verificar uma relação de proporção entre essas grandezas uma vez que temos:

• Para mais construtores conseguimos construir os mesmos metros de muro e isso em menos tempo. Aqui estabelecemos que a quantidade de construtores é proporcional a quantidade de muro construído.
• Em um mesmo tempo de 3 dias se tivermos menos construtores do que 10 conforme dito no enunciado veremos que haverá menos do que 7 metros de muro. Logo, segue que essa análise estabelece que a quantidade de construtores é inversamente proporcional a quantidade de dias de obra.
• Por fim, veja que se fixarmos a quantidade de muro , por exemplo 14 metros, veremos que é necessário mais construtores para efetuarmos essa obra no tempo de 3 dias ou mais dias de obra se a quantidade de construtores for fixa também. Então, temos uma proporcionalidade entre quantidade de muro e tempo de obra e quantidade de construtores.

Consequentemente, da análise de proporcionalidade feita podemos identificar que existe uma constante k que é:

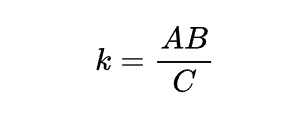
De posse disos, podemos então ver que temos tudo para usarmos a regra de três composta. Na verdade, a construção acima é tudo que você precisa para resolver qualquer problema. Pois em geral, problemas desse assunto envolvem algumas aplicações que pedem a nós para verificarmos como o conjunto de grandezas se modificará perante a alteração de uma delas. Em virtude disso, podemos usar então a constante k para conectar um cenário inicial com um final de modo a termos a seguinte igualdade.

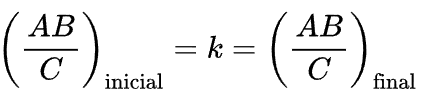
Avaliando um caso prático de regra de três composta

Vamos então determinar a quantidade de construtores necessária para construir 49 metros de muro num tempo hábil de 10 dias. Bom como já temos uma relação para regras de três basta aplicarmos as condições iniciais que temos e então segue que o faremos o problema da seguinte forma.

e agora serão necessários 21 pedreiros e assim concluímos a solução do problema.

Referências

1. IEZZI, Gelson; DOLCE, Osvaldo; DEGENSZAJN, David; PÉRIGO, Roberto. Fundamentos da Matemática Elementar: Volume Único. São Paulo: Atual, 2019.
2. GIOVANNI, José Ruy; CASTRUCCI, Benedito; GIOVANNI JR., José Ruy. A Conquista da Matemática: Volume Único. São Paulo: FTD, 2018.
3. DANTE, Luiz Roberto. Matemática Contexto & Aplicações: Volume Único. São Paulo: Ática, 2019.
4. BONJORNO, José Roberto; GIOVANNI, José Ruy. Matemática Fundamental: Uma Nova Abordagem. São Paulo: FTD, 2018.