Neste artigo descreveremos um sistema de coordenadas introduzido por Newton, denominado sistema de coordenadas polares, que é mais conveniente para muitos propósitos, principalmente quando o intuito é calcular integrais duplas e integrais triplas.
Escolhemos um ponto no plano chamado polo (ou origem) e está rotulado de O.
Então desenhamos uma meia linha começando em O, chamada de eixo polar. dessa forma, esse eixo é geralmente desenhado horizontalmente para a direita e corresponde ao eixo x positivo nas coordenadas cartesianas.
Se P for qualquer outro ponto no plano, seja r a distância de O até P e seja o ângulo (geralmente medido em radianos) entre o eixo polar e a reta OP, como na Figura 1.

Assim, o ponto P é representado pelo par ordenado (r, θ) e r, θ são chamados coordenadas polares P.
Usamos a convenção de que um ângulo é positivo se for medido no sentido anti-horário a partir do eixo polar e negativo se for medido no sentido horário.
Se P = O, então r = 0, e convencionamos que (0, θ) representa o polo para qualquer valor de θ.
Estendemos o significado de coordenadas polares (r, θ) para o caso no qual r é negativo convencionando que, como na Figura 2, os pontos (–r, θ) e (r, θ) estão na mesma reta passando por O e estão à mesma distância |r| de O, mas em lados opostos de O.

Se r > 0, o ponto (r, θ) está no mesmo quadrante que q; se r < 0, ele está no quadrante do lado oposto do polo. Observe que (–r, θ) representa o mesmo ponto que (r, θ + p).
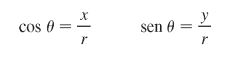
Assim:

A Equação 2 permite encontrar as coordenadas cartesianas de um ponto quando as coordenadas polares são conhecidas.
Portanto, Para encontrar r e θ quando x e y são conhecidos, usa-se as equações

Exemplo de coordenadas polares:
Converta o ponto (2, θ/3) de coordenadas polares para cartesianas
Solução






