Para iniciarmos o assunto de integrais duplas, vamos considerar a figura 1, de modo que: Seja f uma função de duas variáveis contínua, não negativa numa região R do plano xOy.
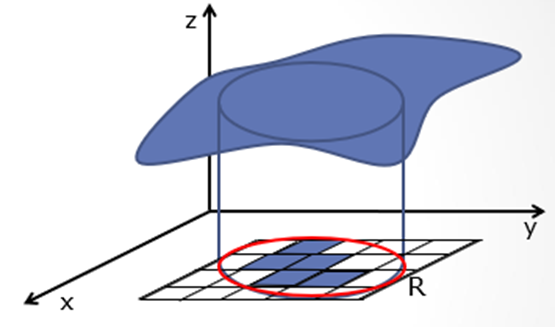
Como desejamos calcular o volume do cilindro limitado pela região R e o gráfico da função f, vamos seguir os seguintes passos
I) Vamos considerar um retângulo de lados paralelos aos eixos Ox e Oy, que contém a região R;
II) Em seguida, vamos dividir esse retângulo em sub-retângulos cujos lados são paralelos aos lados do mesmo.
III) Por fim, excluimos os sub-retângulos que possuam pontos fora da região R.
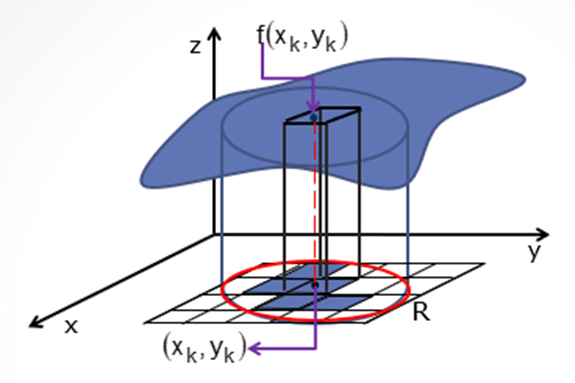
De modo que também vamos supor que restaram n desses sub-retângulos.
Assim, o próximo passo é representar a área do k-ésimo sub-retângulo por ΔAk e seja (xk, yk) um ponto desse sub-retângulo.
Desta forma, o volume do paralelepípedo de área da base ΔAk e altura f (xk, yk) é decerto igual a:
A soma dos volumes de todos os paralelepípedos retângulos cujas bases são os n sub-retângulos é dada por:
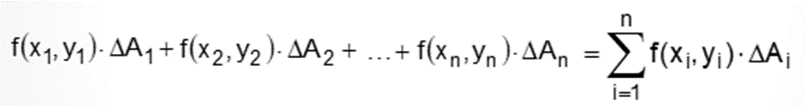
Sendo que está soma é chamada de “soma de Riemann”.
Observe que quando se faz o máximo das ΔAi tender a zero, a soma de Riemann vai se aproximar do volume da porção do espaço compreendida sob o gráfico de f(x,y) e acima da região, de modo que:
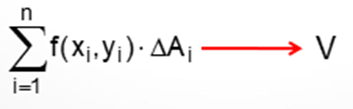
Definição 1
Seja f uma função de duas variáveis, contínua não negativa numa região R do plano xOy.
Então o volume do sólido compreendido entre a superfície z = f(x,y) e a região R é definido por:

Definição 2
Seja f uma função de duas variáveis definida na região R. Assim, temos a definição de integrais duplas de f(x,y) em R o limite:
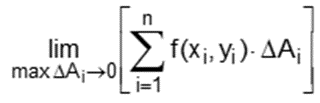
Se esse limite existe e é finito.
Assim, temos a seguinte notação:
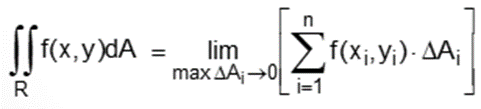
Observe que se a função f for contínua não negativa na região R, desta forma:

Propriedades das Integrais Duplas:
Sejam f(x,y) e g(x,y) funções integráveis na região R e k um número real, então:






