Nesse artigo, vamos ver como resolver integrais por partes. Bem galera, hoje nesse artigo da MeuGuru vamos ver como resolver integrais de funções de uma variável. Em particular, vamos nos ater a um tipo especial de integrais, as quais são as chamadas integrais por partes. Nesse sentido, cola comigo e vem ver esse assunto que vamos desmistificar esse conteúdo de uma vez por todas.
Método para resolver integrais por partes
Primeiro de tudo, vamos entender o método para resolver integrais por partes. Para isso, vamos começar o problema vamos considerar duas funções v(x) e u(x). Além disso, vamos considerar que essas duas funções são suficientemente regulares (isso assegurará que não estaremos cometendo nenhum pecado matemático). Nesse sentido, vamos calcular a derivada do produto dessas funções, nesse sentido teremos o seguinte

com isso em mãos, vamos integrar a expressão acima, desse modo teremos o seguinte

a primeira integral acima, que está do lado esquerdo da integral pode ser facilmente calculada, na verdade, ela é exatamente o produto das funções u e v e isso decorre diretamente do teorema fundamental do cálculo. Com isso, vamos ter o seguinte

Agora, podemos ajustar o último termo acima para termos o seguinte. Com isso, teremos a seguinte expressão
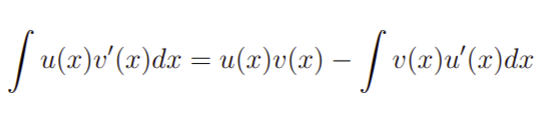
Em particular, essa expressão é exatamente a fórmula para integrais por partes. Em geral, tendo em mãos essa fórmula podemos calcular quaisquer integrais por partes. Nesse sentido, é muito importante que você tenha em mente essa igualdade e carregue-a junto com você na hora das suas avaliações. Bom, tendo esse entendimento teórico em mãos, podemos passar para um exemplo resolvido que irá ajudar você a entender a como resolver essas integrais.
Exemplo resolvido de uma integral por partes
Vamos, agora, resolver um problema de integrais por partes. Em particular, vamos nos ater a integral da função f(x) = ln(x). Em suma, essa integral é não elementar, ou seja, não é resolvida através de métodos simples e sequer possui alguma função que faça esse processo ser elementar. Então, veja que nosso problema é o seguinte
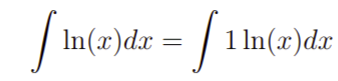
Agora, vamos resolver esse problema passo a passo. Nesse contexto,

onde C é uma constante de integração por estarmos trabalhando numa integral indefinida.
