Nesse artigo, vamos estudar o pêndulo simples. Decerto, esse objeto físico é um dos modelos mais importantes no estudo de oscilações da Física 2. Tendo isso em vista, entender esse modelo torna-se algo fundamental nessa cadeira de física. Portanto, vem comigo que hoje vamos acabar com as dúvidas sobre os pêndulos simples.
Entendendo o que é o pêndulo simples
O pêndulo simples constitui um dos objetos físicos mais interessantes no contexto de movimentos oscilatórios. De fato, esses objetos permitem uma ótima estimativa da aceleração gravidade na terra. Além de que, são sistemas físicos que, sob certas condições, desempenham um movimento harmônico simples.
Tendo isso em vista, vamos caracterizar esse objeto físico. Com efeito, um pêndulo simples consiste essencialmente numa quantidade de massa m, pontual, localizada na extremidade de uma fio rídigo, com massa desprezível e inextensível de comprimento l que possui a outra extremidade fixa num ponto O. Em suma, essa descrição pode ser compactada na Figura 1.
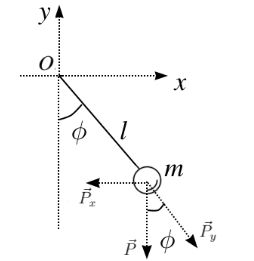
O pêndulo como MHS
Um dos pontos que fazem esse modelo ser tão significativo é que sob uma certa condição o pêndulo simples desempenha um movimento harmônico. Isto é, as oscilações ocorrem todas ao mesmo tempo. Nesse sentido, vamos mostrar de fato que esse sistema físico pode ser tratado como um MHS.
Descrição das forças e torções
Para isso, vamos considerar a Figura 1. Nela, temos as informações das forças que agem sobre a massa m, em particular, as componentes da força peso são as seguintes

Além disso, é importante vermos que o movimento da massa m na Figura 1 é, essencialmente, uma rotação na componente x. Logo, aqui surge uma torção/ um torque o qual é calculado como sendo a massa vezes a aceleração angular do corpo.
Sabendo que, s = ao deslocamento do arco formado pela trajetória da massa temos a seguinte expressão para o torque

onde ‘ denota a derivada em relação ao tempo. Agora, com isso temos que o torque é expresso em termos do angulo phi. Em verdade, essa é a única variável necessária para entendermos como o pêndulo irá comportar-se.
Relacionando os torques e obtendo a equação de movimento
Bom, de posse disso, podemos usar a segunda lei de Newton para rotações de modo a termos o seguinte desenvolvimento no eixo x.
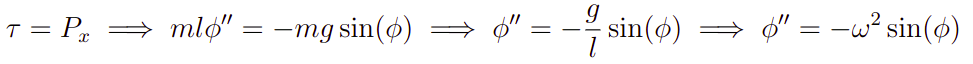
Com isso, obtemos a equação para o pêndulo. Todavia, essa é uma EDO não linear, a saber, essa expressão possui uma solução analítica a qual é obtida por meio das funções elípticas de Jacobi.
Entretanto, vamos linearizar essa expressão. Com efeito, vamos aplicar a aproximação de pequenas angulações. Decerto, no regime em que os ângulos \phi são pequenos é possível obter a seguinte aproximação
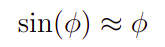
Sob essa aproximação, a dinâmica do pêndulo fica regida pela seguinte equação diferencial
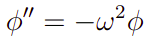
o termo omega ao quadrado que aparece corresponde a fração g/l da Expressão 4. Através dessa demonstração, fica evidente que no regime de pequenas oscilações esse sistema físico é análogo ao MHS, logo, sua solução segue o descrito no artigo.
Determinação do período – O isocronismo das oscilações
De fato, com isso estudar o pêndulo se resume a estudar o MHS. Entretanto, há um resultado significativo que surge nesse sistema. Em suma, a aproximação feita na Expressão 4 é algo significativamente relevante e guia o sistema ao isocronismo das oscilações.
Ou seja, aproximar a dinâmica do pêndulo para pequenos ângulos faz com que o período de cada oscilação seja a mesma. De fato, é exatamente isso que a palavra isocronismo carrega, uma vez que o prefixo iso vem de igual e o sufixo de chronos de tempo.
Mas, essa análise pode ir além da explicação qualitativa e valer-se de forma quantitativa. Com efeito, vamos explicitar o período do pêndulo simples e mostrar que essa quantidade é constante, para isso basta ver o seguinte desenvolvimento

Em que, relacionamos o período e frequência angular através do já estudado movimento circular. Além disso, veja ainda um fato curioso: o período do pêndulo não depende da sua massa mas apenas do comprimento do fio.
Em verdade, esse resultado é primoroso e por conta dele que conseguimos usar o pêndulo para obtenção do valor da constante g. Uma vez que o período T e o comprimento l podem ser facilmente medidos em laboratório.
Com isso, chegamos ao fim de mais um artigo gurunauta, espero que esse artigo tenha sido útil para você. Mas, lembre-se sempre de que na MeuGuru sempre temos um Guru especial para te ajudar com os perrengues da universidade.
