Nesse artigo, você vai conhecer o movimento harmônico forçado. Bem gurunauta, esse artigo é uma extensão do nosso primeiro artigo que falamos sobre o movimento harmônico simples, ou MHS. Agora, vamos ver outro tipo de oscilação: as oscilações forçadas
Então, prepara o caderno e a caneta que hoje vamos ver uma generalização do movimento harmônico simples.
As oscilações forçadas: Introduzindo uma ação externa no MHS
O ponto de partida para entendermos as oscilações forçadas é o próprio MHS. Mais precisamente, vamos considerar, novamente, o modelo de um oscilador harmônico conforme a Figura 1.
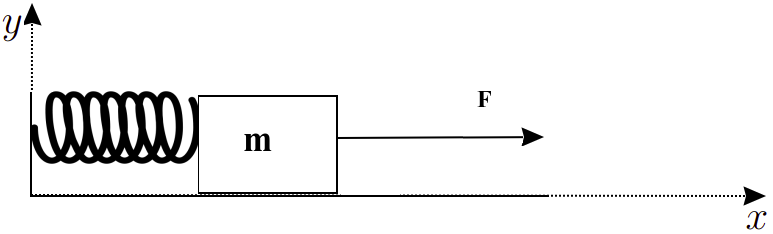
Em geral, determinar a dinâmica do oscilador da Figura 1 é feito através da segunda lei de Newton. Nesse sentido, podemos escrever as forças que atuam no bloquinho, as quais são:
- A força elástica que vem do fato do bloco estar preso a uma mola essa que obedece a lei de Hooke. Ou seja, a força é f = -kx,
- A força Externa F, que é uma ação causada por algum agente que interferiu no bloco.
Com isso, ao usarmos a segunda lei de Newton obtemos o seguinte

onde
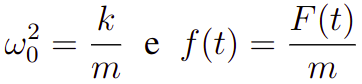
Onde omega0 é o que chamaremos aqui de frequência natural, a qual corresponderá a frequência do oscilador. De fato, essa convenção é importante visto que consideraremos, na seção a seguir que a força f(t) também terá uma frequência de oscilação.
Agora, note que o lado esquerdo da igualdade da Expressão 1 é exatamente o oscilador harmônico simples. Ademais, é importante vermos que introduzir uma força F(t) reduz o problema, matematicamente, a estudarmos uma não homogeneidade na equação diferencial do oscilador harmônico.
Tipos de forças f(t)
Um ponto importante a falarmos aqui é sobre como é o tipo de expressão da força externa f(t). Em verdade, as possibilidades aqui são infinitas, visto que f(t) é apenas uma força qualquer que age sobre o bloquinho. Entretanto, usualmente é considerado dois tipos de forças, as quais são
- Forças oscilatórias,
- Forças impulsivas.
O primeiro tipo é o que nos iremos nos ater nesse artigo. Em verdade, essas forças podem ser escritas da seguinte forma
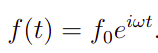
aqui, f0 é a amplitude de uma onda cujo frequência de vibração é omega. Note que, a Expressão 3 é complexa, todavia, a introdução dessa forma é estratégica visto que ao fim do desenvolvimento consideraremos apenas a parte real da solução.
Além disso, é importante dizermos que não vamos considerar as forças impulsivas aqui. Em particular, essas forças são associadas a agentes que atuam substancialmente rápido no sistema e são frequentemente vistas em osciladores harmônicos nos circuitos elétricos. Todavia, a forma para a solução desse problema emprega a transformada de Laplace.
Além disso, as forças oscilatórias podem ser frequentemente vistas na natureza, assim, tornando-se um tipo muito importante de agente externo nos osciladores a serem estudados.
Regime estacionário do movimento harmônico forçado
Agora, tendo o conhecimento da força externa oscilante sobre o sistema do oscilador harmônico vamos obter a expressão da dinâmica do oscilador harmônico forçado. Com efeito, nosso objetivo será não ter uma expressão geral para o movimento mas uma forma particular.
De fato, essa particularidade vem da ideia física de que, após um determinado tempo o sistema físico deverá ser dominado pela ação do agente externo. Assim, faz-se necessário que tenhamos uma solução para o regime estacionário a qual é obtida buscando uma solução que tenha um rosto familiar a expressão da força externa, por exemplo
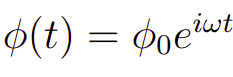
Levando a Expressão 4 na Expressão 3 teremos o seguinte desenvolvimento

Daí, tomando a parte real da expressão 4 com phi0 determinado na expressão 5 temos a seguinte solução estacionária

Note que, inserimos o módulo no denominador, isso é apenas uma convenção. Além disso, veja que se a frequência omega da força se aproximar da frequência de oscilação natural omega 0 a expressão para x(t) tenderá ao infinito. Com efeito, isso é interpretado, fisicamente, como o caso em que o sistema deixa de ser oscilante. Em suma, esse fenômeno é chamado de ressonância e exploraremos ele melhor num artigo futuro.
Ademais, a expressão 6 nos dá o entendimento da dinâmica no regime estacionário de x(t). Assim, conseguimos compreender e obter a forma matemática do problema.
E com isso, chegamos a mais um artigo gurunauta. Mas olha, fica ligado nas novidades da MeuGuru e no blog que logo logo vamos postar mais textos sobre oscilações, em particular, vamos fazer um artigo só sobre a ressonância que comentei e sobre as oscilações amortecidas.
