Nesse artigo vamos falar sobre as séries de Fourier. De fato, as séries de Fourier são uma temática muito importante nas ciências exatas. Além disso, por vezes, são temidas nos cursos de cálculo avançado tendo em vista várias complicações naturais que emergem no desenvolvimento do assunto.
Bom gurunauta, tendo isso em vista, nesse artigo, nós da MeuGuru vamos buscar elucidade esse assunto. Vem comigo que hoje vou te passar as ideias gerais sobre essa matéria, além disso, vamos até resolver um exemplo passo a passo com você.
Ideia geral das séries de Fourier
Para que você possa entender a ideia por trás das séries de Fourier é necessário pensarmos e refletirmos um pouco sobre aproximações de funções. De fato, a noção de aproximarmos funções complicadas por outras mais simples já acontece na matemática em vários cenários, em particular, podemos ver isso nas séries de Taylor.
Entretanto, aqui nosso objetivo é aproximar uma dada função f(x) em termos de senos e cossenos. Assim, nessas séries aproximamos a função f(x) por meio de funções periódicas. Tendo isso em vista, podemos ver que esse método valoriza os aspectos periódicos da função e assim sendo extremamente útil para eliminarmos ruídos em funções quase periódicas.
Apresentando as séries de Fourier
Então, entendendo a motivação por trás dessas séries vamos agora nos ater ao aspecto matemático dessas séries. Com efeito, a série de Fourier de uma função f(x) cujo periódo seja L (as vezes é comum encontrar a notação L-periódica) é a seguinte
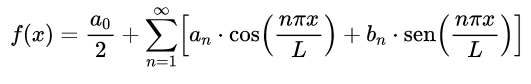
onde os termos an e bn são os chamados coeficientes de Fourier e são dados, respectivamente, por

para todo n natural. Os coeficientes de Fourier podem ser obtidos usando propriedades de ortogonalidade das funções cosseno e seno.
Um exemplo
Agora que conhecemos e entendemos a ideia de uma série de Fourier, vamos determinar a série para uma função simples. Em particular, para a função f(x) = x definida de -L a L onde L é um número positivo que é o período da função.
Com efeito, o procedimento geral para determinarmos a série de Fourier de uma função é, primeiro, calcular os coeficientes de Fourier associados a ela. Nesse sentido, teremos que
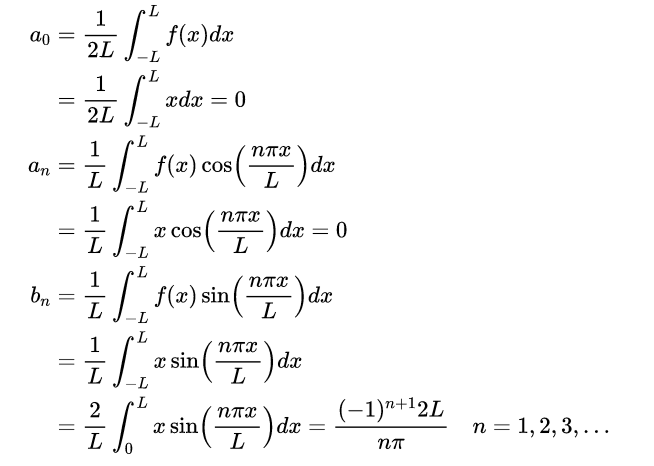
Com isso, agora para obtermos a série de Fourier basta aplicarmos os coeficientes obtidos acima na expressão geral da série de Fourier. Com efeito, teremos o seguinte então .

E assim, determinamos analiticamente a expressão para a série de Fourier desejada.
Comentando algumas aplicações importantes
As séries de Fourier são, de fato, importantes. Entretanto, apenas falar e reafirmar isso não é suficiente para que eu consiga te convencer disso não é mesmo gurunauta?. Bom, então eu separei algumas aplicações muito interessantes delas, confere aí.
- Soluções de Equações Diferenciais Parciais como a EDP da onda, calor e Schrödinger
- Wavelets,
- Mecânica quântica,
- Jogos online.





