O Teorema do valor médio (TVM) é um dos teoremas mais importantes no cálculo 1. De fato, no início do estudo do cálculo diferencial somos apresentados a vários resultados importantes, dentre estes o Teorema do valor intermediário e o TVM. Nesse sentido, hoje nós da MeuGuru vamos explorar o TVM, vamos explicar ele de vez para que você consiga entender esse assunto e arrasar em suas provas de cálculo.
O que é o Teorema do valor médio ? (TVM)
Primeiramente, vamos entender o que de fato é o Teorema do valor médio. Com efeito, esse teorema é um resultado que relaciona a derivada de uma função contínua e diferenciável com os extremos de um intervalo onde a função está definida. Em verdade, o enunciado desse teorema pode ser posto a seguir.

Ou seja, assim como o Teorema do valor intermediário o TVM é também um resultado de existência.
Em suma, esse resultado pode ainda parecer um resultado simples e até mesmo inocente. Entretanto, esse resultado tem várias nuances que o fazem ser um queridinho dos professores em provas de cálculo. Por conta disso, vamos explorar as duas grandes consequências desse Teorema:
- O sentido geométrico
- As aplicações em crescimento/descrescimento e concavidade das funções.
Interpretação geométrica do TVM
Naturalmente, a noção de derivada é construída tendo em vista um sentido geométrico. Com efeito, a derivada, naturalmente, determina a inclinação da reta tangente num ponto da curva f(x). Seguindo essa linha, o TVM estabelece um resultado geométrico análogo, sendo esse associado a reta secante a curva y=f(x).
Em verdade, o TVM nos diz que a reta tangente no ponto c garantido pelo TVM é paralela a reta secante que liga os pontos (a,f(a)) e ponto (b,f(b)). Decerto, podemos esquematizar essa interpretação conforme a Figura 1.
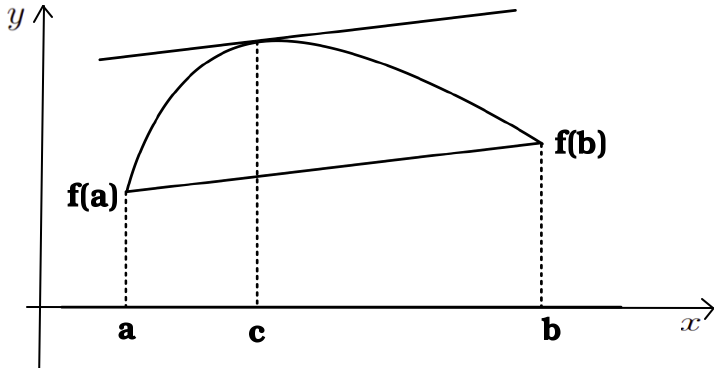
Aplicações do teorema do valor médio
Agora, vamos explorar algumas aplicações do TVM. Em verdade, essas aplicações são muito importantes no estudo do cálculo, em particular, essas serão primordiais para o esboço dos gráficos. Nesse sentido, vamos exibir esses resultados através de Teoremas, com efeito, o primeiro desses é.

Além disso, o TVM ainda assegura o seguinte resultado sobre a concavidade das funções, o qual é posto através do seguinte Teorema.

Nosso objetivo aqui não é se a ter as formalidades ou mesmo a provar esses resultados. Em verdade, aqui estamos querendo apenas dar a importante noção da relevância do TVM. Entretanto, caso você queira se debruçar sobre esses resultados basicamente basta aplicar o resultado do TVM tendo em vista que você conseguirá garantir que f'(c) = f(b)-f(a) / b – a para todo c e para todo intervalo (b,a).





