Nesse artigo, vamos falar sobre o cálculo de volumes com integrais.
Fala gurunauta, dessa vez vim aqui para te ajudar com aqueles problemas sobre cálculo de volume de um sólido com integrais. Isso mesmo, no post de hoje, vamos garantir que você entenda, de uma vez por todas, os dois principais métodos para o cálculo de volume de sólidos com integrais. Portanto, vêm comigo e para que juntos, nós risquemos a palavra reprovação do seu vocabulário.
Cálculo de volumes: Método dos discos
A primeira forma de calcular volumes com integrais é através do chamado método dos discos. Nesse método, a ideia é imaginar uma função f(x) que é rotacionada em torno do eixo x. Daí, calcula-se a soma de todos os discos que formam-se na região rotacionada. A Figura 1, ilustra essa esquematização.
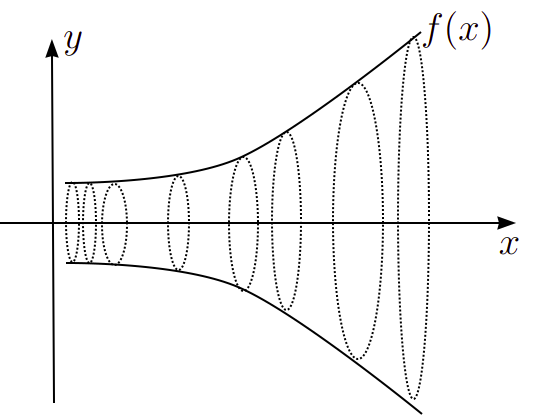
O método dos discos, permite, então o cálculo do do sólido assim gerado. Em suma, o que você precisa ter em mente é como esse volume é calculado. De fato, ele é dado por
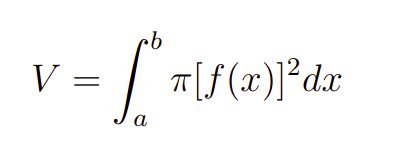
onde, a e b são os extremos de integração e o integrando é pi vezes f(x)^2. Em verdade, esse integrando é na verdade a área de um circulo dos discos que compõem o método, cujo raio é r=f(x) . Analogamente, você pode ter uma rotação em torno do eixo y, nessas condições o volume passa a ser dado por:
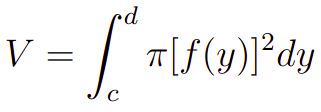
Cálculo de volumes: Método das cascas cilíndricas
O segundo método, igualmente importante, é o método das cascas cilíndricas. Dessa vez, vamos imaginar o seguinte problema. Consideremos uma função f(x) que será rotacionada em torno do eixo y como mostrado na Figura 2.

Nesse caso, nós vamos trabalhar com a parte lateral desses cilindros. Talvez, seja difícil para você ver, mas confere a Figura 3, que vai ficar bem mais claro para você.

Com isso, vamos calcular a o volume total. Consequentemente, esse volume será a soma de todas as áreas laterais obtidas. Ou seja, no contexto de integrais, teremos que o volume obtido por esse sólido será dado por

onde o integrando, corresponde a área lateral de um cilindro com raio r=x e altura h=f(x).
Por fim, lembre-se de sempre contar com a MeuGuru para te salvar da reprovação. Aliás gurunauta, confira também algumas aplicações das derivadas que podem te ajudar na prova de cálculo 1.





