Fala gurunauta, nesse artigo vamos ver como você pode calcular o volume máximo no cálculo 1. Em verdade, o problema de determinar o volume máximo no cálculo 1 é um dos problemas clássicos do cálculo diferencial. Tendo isso em vista, nesse artigo vou resolver um exercício em que vamos determinar o volume máximo de uma caixa sob algumas condições. Cola comigo e com a MeuGuru e vem ver esse exemplo que vai super te ajudar.
Apresentando o problema: uma caixa
Vamos considerar uma caixa de base retangular, com tampa e altura h assim como mostrado na Figura 1.
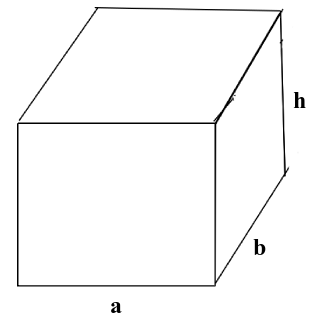
Ademais, consideremos, ainda, que caixa da Figura 1 tem a restrição de que a altura h e a área lateral da caixa seja constante e igual a A. Tendo isso em vista, vamos mostrar como calcular o volume máximo.
Como calcular a função volume
Inicialmente, vamos obter as funções que descrevem nosso problema, em suma, faremos algumas etapas de modelagem. Com efeito, vamos partir da hipótese de que a área lateral é constante e vale A, matematicamente, isso é escrito da seguinte forma
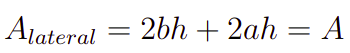
onde cada termo está multiplicado por 2 por termos duas faces paralelas de dimensões b e h e a e h. Além disso, é conhecido que o volume de uma paralelepípedo (formato da caixa) é da seguinte forma

Com isso, deveremos obter a função volume. Para isso, usaremos a restrição da área lateral da seguinte forma:


Com isso, conseguimos obter uma expressão de V em termos de a. Logo, podemos tratá-la como uma função do primeiro grau. Nesse sentido, o problema de achar o volume máximo da caixa passa a ser determinar o ponto de máximo da função V(a). Vamos fazer isso a seguir.
Como calcular o volume máximo
Tendo em mãos a função V(a), vamos determinar seus pontos críticos que são os pontos “a” onde a derivada de V(a) se anula, pois, esses pontos são candidatos a máximos críticos. Para isso, calculamos a derivada de V em relação a “a”

o cálculo do ponto crítico a é eito a seguir. Com isso, temos o seguinte

Portanto, temos um único ponto crítico. De posse disso, podemos verificar se é ponto de máximo de V, para isso, calculamos a derivada segunda. Com efeito

Uma vez que essa é estritamente negativa, o teste da derivada segunda garantirá que a = A/4 é um ponto de máximo e logo é o ponto que maximiza V. Com isso, agora vamos determinar o volume máximo. De fato, basta substituirmos o valor de a na expressão de V(a), com efeito

Dessa forma, obtemos o volume máximo.
