A “função” delta de Dirac é uma importante ferramente matemática para o tratamento de diversos problemas em física, engenharia e matemática avanaçada. De fato, esse conceito surge inicialmente na Física, com os trabalhos do prêmio Nobel Paul Dirac. Entretanto, seu poder logo ganhou notorieade nas aplicações e tornou-se o ponta pé inicial para o desenvolvimento da teoria das distribuições, que generalizam a noção usual de funções.
Tendo isso em vista, hoje a MeuGuru preparou um artigo especial para você entender esse conceito e conhecer algumas propriedades importantes da delta de Dirac. Então gurunauta, vem comigo que hoje vamos adentrar num ambiente novo com muita matemática diferente da que estamos acostumados, mesmo nos cursos de cálculo.
A delta de Dirac
Antes de tudo, é importante entendermos por que sempre estamos nos referindo a delta como uma “função” entre parênteses. De fato, a definição formal de função nos leva a considerar um objeto matemático que associa cada termo do domínio a um único valor no contradomínio. Entretanto, a delta de Dirac torna isso impossível de ser satisfeito. Com efeito, definamos a delta de Dirac da seguinte forma.
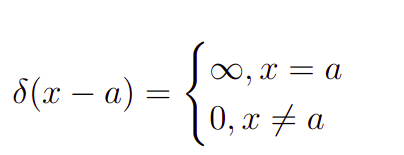
Em particular, sequer conseguimos ter uma representação gráfica para esse novo objeto matemático que estamos conhecendo. Com efeito, no início de sua concepção pelo físico teórico Paul Dirac, temos uma representação dessa “função” como uma seta que apontava para cima, assim como mostramos no ícone desse artigo.
Motivações para o surgimento da delta de Dirac e distribuições
As origens da delta de Dirac aparecem nos trabalhos de Paul Dirac na compreensão da teoria quântica. Entretanto, seus desenvolvimentos urgem em diversas áreas, em particular, a partir da definição da delta, é possível associá-la aos chamados fenômenos impulsivos.
De fato, a ideia de ter uma grandeza que toma um valor suficientemente grande num ponto pequeno é ótima para a modelagem de diversos problemas como
- Forças impulsivas em sistemas mecânicos,
- Introdução de uma corrente em circuitos elétricos.
Ademais, ramos como a teoria da probabilidade e a própria Teoria Quântica de Campos se valem dessa “função” para a descrição de estados de partículas em cenários quânticos e relativísticos.
Entretanto, dada sua complexidade é necessária uma uma teoria muito mais robusta do que apenas o cálculo diferencial. Em especial, o arcabouço matemático que assegura o correto emprego desses objetos é a chamada teoria das distribuições que foi concebida por Schwartz no século XX (sim, isso é bem recente). Em virtude dessa teoria, o matemático Schwartz foi agracido com a maior honraria da matemática: A medalha Fields.
Como estudar a delta de Dirac?
Tendo em mãos a chamada Teoria das distribuições, podemos então passar a estudar a delta de Dirac com certa segurança de não estarmos cometendo nenhum pecado matemático. Em verdade, essa teoria nos leva a noção de função teste, a qual não vamos nos deleitar muito. Nesse contexto, vamos nos ater apenas as ideias básicas que serão suficientes a nós.
A ideia, em geral, é transladar a construção da delta de Dirac para funções, ou melhor, sequências de funções. Essas, por sua vez, são funções que possuem as propriedades que definem a distribuição de Dirac. Em particular, podemos citar alguns exemplos dessas funções testes, com efeito.

Note que nesse caso, a medida que n tende ao infinito, teremos que a delta tenderá ao infinito também. Ademais, um importante exemplo é associado a distribuição guassiana que é mostrada a seguir.

Para que você tenha uma melhor compreensão visual do assunto, basta ver o gráfico a seguir que mostra o que ocorre para alguns valores de n.
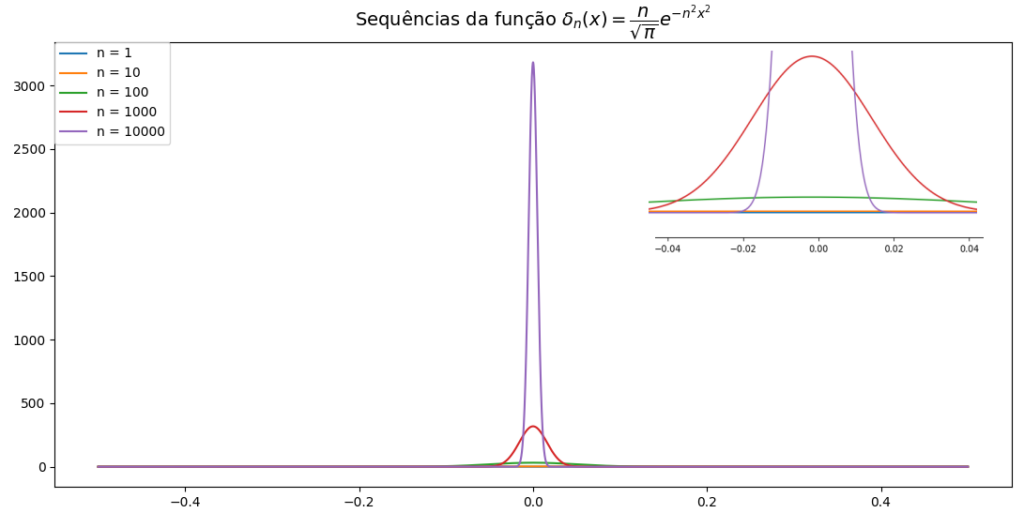
Algumas propriedades importantes
Quando nos referimos a essa “função” é interessante citarmos duas importantes propriedades. A primeira propriedade, é associada a integração dessa distribuição sobre todo o espaço que está definida. Em verdade, essa nos diz que, por definição, devemos ter que.

esse resultado é de grande utilidade, em particular, na teoria das probabilidades. A segunda, aparece quando consideramos uma função f(x) contínua que se anula nos infinitios, com isso, segue que temos a seguinte propriedade:

essa propreidade pode ser facilmente verificada usando integração por partes e a propriedade citada anteriormente. Essa última é chamada, informalmente, de propriedade de filtragem da função delta de Dirac.
