Nesse artigo, vamos falar de derivadas e taxas relacionadas, para que você consiga resolver esses problemas e garantir a aprovação no semestre.
Mais uma vez estamos aqui gurunauta, com mais um artigo para te salvar da reprovação. Dessa vez, o assunto será derivadas e taxas relacionadas. Em especial, mostraremos como você pode resolver esse tipo de problema em poucas etapas. Então, já se acomode e confira esse artigo escrito, especialmente, para você.!
Derivadas e problemas de taxas de variação
A derivada é um dos conceitos mais importantes que você vai aprender nos cursos de cálculo da sua faculdade. De fato, ela possui diversas aplicações em física, química, biologia e engenharia. Logo, conhecer essa ferramenta é extremamente importante para sua formação.
Dentre essas aplicações, há um destaque para problemas que envolvem as chamadas taxas de variação. Basicamente, nesses problemas você que entender como algo irá mudar se outras componentes do sistema também mudam. Por exemplo, imagine que você queira determinar como a posição de um corpo está variando ou como sua velocidade varia. Para isso, você pode calcular a derivada da função posição e da função velocidade.
Por outro lado, há problemas em que você deve determinar como taxas que estão associadas irão variar. Por exemplo, pensa no volume de uma esfera, em que o raio está crescendo a uma uma taxa de 2m/s. Nesse caso, o volume também crescerá, porém, com uma taxa diferente da do raio.
De fato, os problemas que envolvem taxas de variação tornam-se essenciais e práticos. Pois, possuem uma forte natureza aplicada, podem ser relacionados a diversos contextos, em especial, na sua prova. Por isso, vou te ensinar a como resolver esses problemas.
Como resolver taxas de variação simples ?
Os problemas com taxas de variação simples são resolvidos de forma imediata, basta você calcular a derivada da função que você tem. No entanto, há uma importante aplicação que você deve conhecer que é na cinemática, e essa é,
- A derivada da função posição s(t) é a função velocidade v(t).
- A derivada da função velocidade v(t) é a aceleração a(t).
- A derivada segunda da função posição s(t) é a aceleração a(t).
Em fórmulas, temos o seguinte:
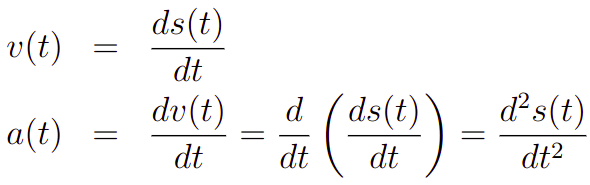
Vamos resolver um problema simples, determinar a velocidade e aceleração de um corpo que se move com s(t) = 2t+3t^2 + cos(t). Nesse caso, teremos que as taxas de variação da velocidade e aceleração serão

Regra da cadeia para derivadas e taxas relacionadas
Agora, vamos considerar o problema das taxas relacionadas. Na verdade, esse é apenas uma extensão do problema anterior. Pois, aqui consideraremos que a função que estamos estudando, f(t), depende de alguma forma de uma função r(t). Nesse caso, para determinarmos como f(t) varia em relação a variável t, devemos usar a regra da cadeia, para termos

É sempre importante destacar isso. As taxas relacionadas são uma boa forma do seu professor cobrar o uso da regra de cadeia, além de misturar com aplicações em problemas e geometria e da física. Por isso, vamos resolver um problema
Como resolver problemas com taxas relacionadas ?
Agora, vamos resolver um problema de taxas relacionadas. Esse problema é um clássico nesse estudo. Vamos determinar como o volume da esfera varia em relação ao raio se o ele for variável em relação ao tempo.
Bom, vamos começar o problema relembrando a fórmula do volume da esfera V de raio r, que é a seguinte

No entanto, nosso problema trata V e r como função de t. Portanto, teremos que
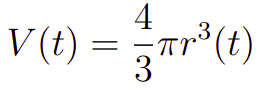
E logo, a derivada do volume em relação ao tempo será dada, pela regra da cadeia, por:
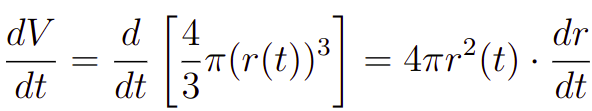
Portanto, se você souber a forma da função r(t), você terá a fórmula explicita de como V varia com t. E apenas com isso você já será capaz de resolver o problema.
Ademais, diversos problemas de taxas relacionadas são resolvidos exatamente dessa forma. Portanto, saber esse exemplo e ter ele em mente será muito bom na hora da sua prova.
Com isso, chegamos ao fim do nosso texto caro gurunauta. Agora é hora de você colocar a mão na massa e arrasar nas provas e, caso tenha dificuldades, lembre-se de contar sempre com a MeuGuru para te ajudar nas suas listas e questões. Até a próxima.
