A eletrostática é uma das áreas iniciais da Física 3. Em verdade, essa disciplina é uma das mais importantes da Física no ensino superior. Não apenas isso, mas é na Física 3 que nós vemos, pela primeira vez, aos conceitos que permeiam o eletromagnetismo. Pensando nisso, hoje nós da MeuGuru preparamos um artigo especial para você gurunauta. Aqui, vamos entender como podemos resolver um problema de eletrostática passo a passo aplicando a um clássico problema dessa disciplina.
Passo 1. Apresentando o problema de eletrostática
Antes de tudo, é important inicialmente, entendermos o problema que vamos atacar nessa solução. Em virtude disso, agora vamos apresentar esse problema. Com efeito, nosso objeto será determinar o campo elétrico num ponto P gerado por uma distribuição de carga superficial. O problema em questão é clássico da eletrostática e pode ser esquematizado de acordo com a Figura 1.
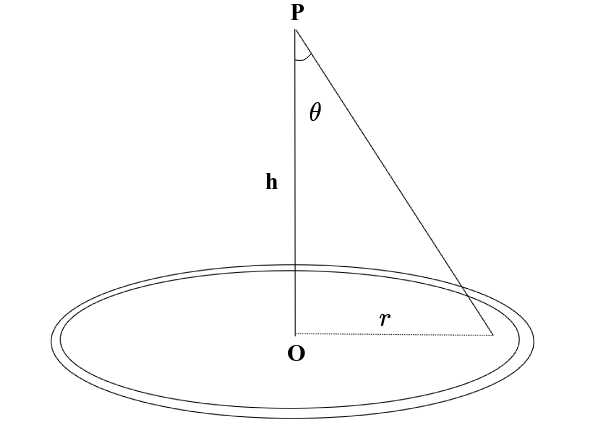
O objetio em si é a determinação do campo elétrico total que age no ponto P. Ademais, sabemos que o disco é carregado com uma carga tota Q e há uma carga de prova no ponto q. Além disso, a carga de prova fica situada numa distância h do disco de área superficial A e densidade de carga homogênea.
Passo 2. Entendendo a geometria do problema
Agora que já temos em mãos o passo 1, vamos nos ater a entender melhor esse problema. Em especial, esse tipo de problema pede, imediatamente, que analisemos a geometria do problema. Nesse sentido, a partir da figura 1 podemos obter a seguinte esquematização.

Com a Figura 2, vemos um pouco melhor a interação entre o campo elétrico da carga pontual e do disco. Entretanto, a partir dessa configuração conseguimos ver que o problema nos dá uma certa simetria. De fato, se olharmos bem as contribuições do campo elétrico são sempre decompostas no eixo vertical e no eixo horizontal.
Todavia, as contribuições do eixo horizontal acabam sendo todas mutualmente canceladas dada a simetria circular do disco, a qua irá sempre produzir uma intração igual de sentido oposto. Por outro lado, a interação na vertical (eixo z) deverá ser dobrada pois cada componente se soma, mutualmente. Assim, obtemos que a expressão geral do campo elétrico deverá ser

onde Ez é a componente do eixo z vertical. Entretanto, essa componente pode ser calculada a partir da decomposição dos vetores. Em especial, infinitesimalmente nós teremos que
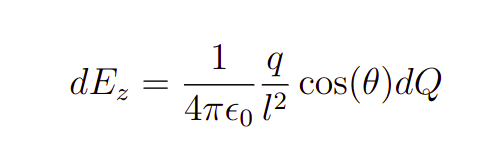
onde dQ é um elemento de carga infinitesimal e l é a distância inclinada da carga até o disco. Aqui, fica evidente a necessidade do entendimento da geometria do problema, o cosseno do ângulo pode ser calculado e é dado por

Passo 3. Grandezas da eletrostática envolvidas
Tendo em mãos os conceitos básicos advindos da geometria do problema, podemos, então, partir para manipular as grandezas da eletrostática envolvidas no problema. Primeiramene, note que podemos estabelecer a seguinte correspondência para Q com a densidade de carga rho do disco

e usando a área a circunferência como sendo A(r) = pir^2, é possível obter, derivando A o seguinte.

Por outro lado, usando o Teorema de Pitágoras temos que l2=r2+h2. Então, podemos usar todos esses resultado e teremos a seguinte expressão para o campo elétrico infinitesimal.

Essa é a expressão para Ez e nosso objetivo é determinar essa grandeza e bem, agora, nosso problema pode ser resolvido simplesmente integrando a expressão acima.
Passo 4. Resolvendo o problema
Como última etapa, basta integrarmos a expressão acima. Ademais, vamos supor que o raio total do disco seja R, deste modo a integral da expressão anterior nos dá o seguinte desenvolvimento.
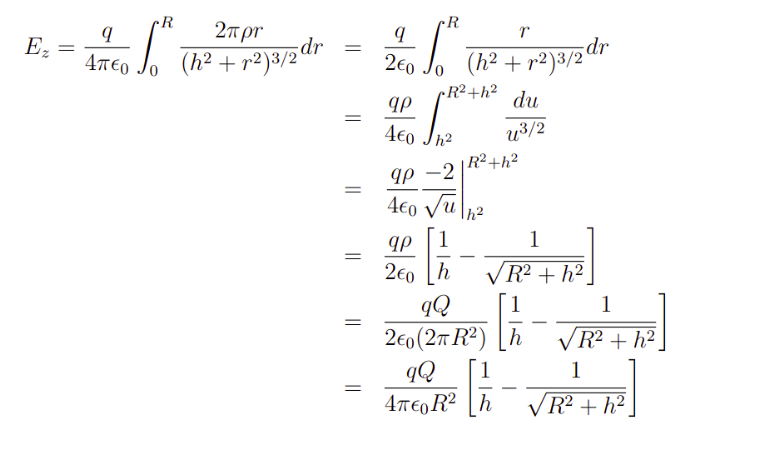
e com isso obtemos o desejado.





