Fala gurunauta, nesse artigo vamos falar sobre as equações diferenciais ordinárias. Em especial, as EDOs de primeira ordem, ou simplesmente, de ordem 1.
Dessa vez, vamos ter mais um texto sobre as equações diferenciais ordinárias. Em nosso primeiro texto, nós falamos de forma geral sobre as EDOs, no entanto, apresentamos o importante conceito de ordem de uma EDO. Tendo isso em vista, chegou a hora de particularizar as coisas e nos ater a alguns casos muito interessantes. Nesse sentido, confere esse texto e garanta a salvação na disciplina de equações diferenciais.
Equações diferenciais ordinárias de ordem 1
As equações diferenciais ordinárias de primeira ordem, ou ordem 1, são caracterizadas por terem apenas a derivada primeira. Logo, se pensarmos, essas equações são o tipo de EDO mais simples que existe. A forma geral de uma EDO desse tipo pode ser escrita por:
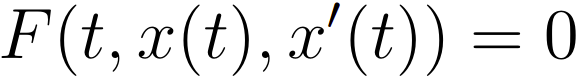
onde a incógnita é uma função x = x(t) e F é uma regra geral que associa os argumentos.
No entanto, há um tipo específico de EDOs de primeira ordem, as equações lineares. De fato, como já sabemos, poucas vezes conseguimos resolver uma equação diferencial, mas, no contexto de ordem 1 e para as EDOs lineares conseguimos obter uma fórmula fechada de solução. Essa fórmula consegue resolver, toda e qualquer EDO linear de primeira ordem. Nesse sentido, é importante conhecermos esse tipo de equação, sua forma geral é a seguinte
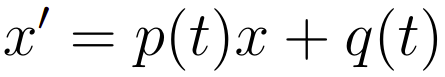
Soluções para as equações diferenciais ordinárias lineares de ordem 1
Conforme mencionado anteriormente, as equações diferenciais lineares de primeira ordem possuem uma fórmula pronta e fechada para qualquer solução. Nesse contexto, conhecer essa fórmula é muito significativo para o estudo e entendimento da teoria das EDOs. Pois, decerto, não há outro contexto para equações diferenciais que possa-se obter uma expressão tão geral.
Então, chega de preliminares, vamos ao que interessa. Vamos considerar um Problema de Valor Inicial (PVI) de primeira ordem, isto é,
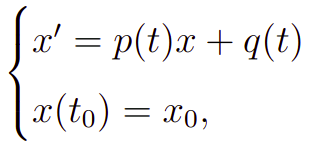

Então, a solução exata para um PVI de primeira ordem, com p(t) e q(t) funções contínuas quaisquer, é dada pela fórmula da variação das constantes que é posta a seguir
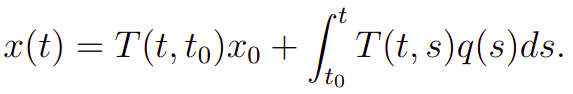
Portanto, conhecendo as duas expressões acima, você é capaz de resolver qualquer PVI que envolva equações diferenciais de primeira ordem.
Bom gurunauta, mais um artigo que chega ao fim. Mas, o conteúdo não para por aqui, confere nossa plataforma MeuGuru e sempre conte com a gente para te ajudar a escapar da reprovação. Mete bronca e tamo junto!





