“Integrais triplas são o análogo de integrais duplas em três dimensões. De certo, elas são uma ferramenta para somar infinitamente grandezas infinitesimais associadas a pontos em uma região tridimensional”.
Preliminarmente, vamos relembrar a definição de integrais duplas:
Seja f uma função de duas variáveis definida na região R. Chama-se integral dupla de f(x,y) em R o limite:


A definição de integral tripla segue os mesmos passos da definição de integral dupla. Observe :
Definição 1
Seja f uma função de três variáveis definida sobre um sólido E.
Chama-se integral tripla de f(x,y,z) em E o limite:

De certo, o limite tem de existir e ser finito.
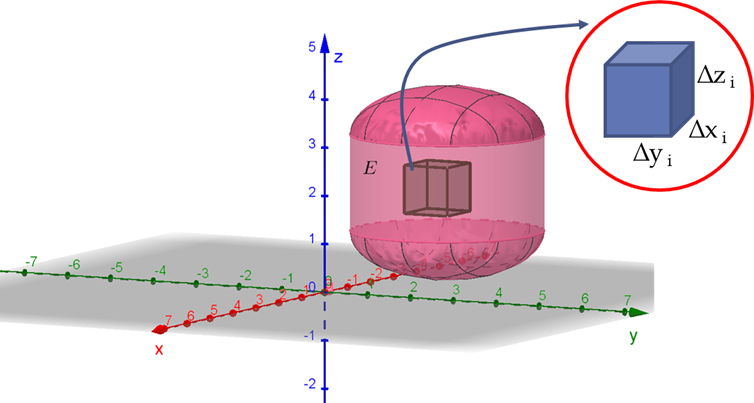
Notação:

Propriedades
Sejam f(x,y,z) e g(x,y,z) funções integráveis sobre o sólido E e k um número real, então temos que:

Cálculo das integrais triplas
1o Caso: O sólido E está contido entre os gráficos de duas funções contínuas de x e y, ou seja,

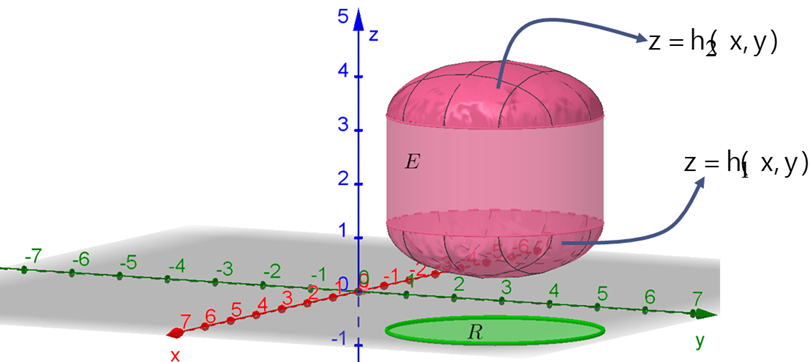
Então, de modo análogo temos as equações:
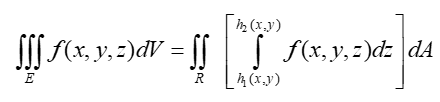
Exemplo 1:

Em síntese, se faz necessário realizar as seguintes observações:
1. Os limites de integração da integral de dentro contêm no máximo duas variáveis;
2. Os limites de integração da integral do meio contêm no máximo uma variável;
3. Os limites de integração da integral de fora precisam ser constantes.
Para calcular áreas de regiões planas R utilizando integrais duplas, assim considerando f(x,y) = 1.

Onde A é a área da região R.
Portanto, podemos calcular o volume do sólido E, considerando f(x,y,z) = 1 .
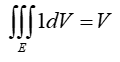
Onde V é o volume do sólido E.





