A equação de Laplace é uma das EDPs mais importantes no contexto da física e da matemática. De fato, há inúmeros problemas relevantes de engenharia que são modelados por essa equação. Em particular, podemos citar o transporte de neutrôns em reatores nucleares e até o comportamento do potencial elétrico de uma distribuição de cargas.
Por outro lado, essa equação aparece como uma das primeiras EDPs que estudamos nos cursos de cálculo avançado. Tendo isso em vista, estudar essa equação e saber resolvê-la é extremamente necessário para um bom rendimento numa prova de cálculo. Em virtude disso, hoje nós dá MeuGuru preparamos um texto especial para você onde vamos sanar, todas as dúvidas possíveis desse assunto.
Então gurunauta, vem comigo que hoje você vai conhecer e aprender a como resolver a EDP de Laplace.
O que é uma equação de Laplace ?
Uma Equação de Laplace, é uma EDP associada ao operador Laplaciano. Em geral, essa equação tem a seguinte forma geral
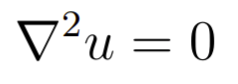
onde u é uma função que é duas vezes diferenciáveis. Essa equação foi nomeada em homenagem ao matemático e astrônomo francês Pierre-Simon Laplace. Em suma, o astrônomo a utilizou para estudar fenômenos astronômicos e gravitacionais no final do século XVIII e início do século XIX.
Como resolver a equação de Laplace ?
Em geral, determinar uma solução para a equação de Laplace pode ser feita de diferentes formas. Ademais, em diversas questões e provas esse será seu grande objetivo, especialmente, nas suas provas. Tendo isso em vista, vamos comentar algumas formas para ter-se soluções dessa equação, a primeira é o método de separação de variáveis que pode ser feito da seguinte forma

E assim, o problema de resolver a EDP de Laplace passa a ser o mesmo de resolver três EDOs de segunda ordem, as quais você pode ver como resolver aqui.
Coordenadas cilíndricas
O operador Laplaciano, pode ser inscrito em diferentes sistemas de coordenadas. Quando mudamos o problema para coordenadas esféricas, passamos a ter um novo desenvolvimento. Nesse casso, a EDP de Laplace fica dada por
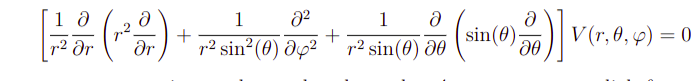
Agora, fazendo a separação de variáveis, analogamente, teremos para funções R e bigtheta que

e obtemos duas equações diferenciais ordinárias, que são

A primeira equação é uma EDO de Cauchy-Euller e sua solução é

Por outro lado, a segunda equação é uma EDO especial, em verdade, é uma EDO de Legendre cujo solução é dada pelos polinômios de Legendre. Ou seja, teremos que a solução da EDP fica dada por

Aplicações da EDP
Podemos elencar algumas das aplicações da EDP de Laplace. Em sua, essa equação de Laplace aparece em diversas áreas da física e da matemática, como na eletrostática, na termodinâmica, na teoria da elasticidade, na teoria do potencial, na mecânica dos fluidos e na teoria dos campos. Ela descreve a distribuição estacionária de um campo escalar em um domínio, ou seja, a distribuição de temperatura, de pressão, de potencial elétrico ou de outra grandeza física que não varia com o tempo.





