Fala gurunauta, hoje vamos falar sobre os números racionais e irracionais. Hoje nós da MeuGuru, preparamos um artigo especial para você. Vamos falar sobre os números, particularmente, os que chamamos de racionais e irracionais. Nosso objetivo vai ser contar um pouco sobre a história desses números e também usá-los como motivação para falarmos sobre técnicas de demonstração.
Então gurunauta, vem comigo e confere esse artigo.
A visão dos gregos sobre os números racionais e irracionais
Antes de tudo, é necessário termos um ponto de início, em particular, esse ponto de partida será a Grécia antiga. De fato, os filósofos e matemáticos já existentes nesse período dedicavam-se, fortemente, a compressão e reflexão sobre um certo tipo de objeto, os quais eram chamados de números. Atualmente, o grande conjunto numérico que nós estudamos é o chamado de reais que é simbolizado por

Entretanto, quando olhamos para a grécia antiga vemos que esse conjunto ainda não existia. Em verdade, para os gregos a noção de número era atrelada a medidas/medições e essa conexão era tão forte que até a matemática poderia ser vista como apenas a geometria. Entretanto, é num problema geométrico que a estrutura dos números dos gregos mostrou-se falha.
Nesse contexto, é possível ver que os números conhecidos pelos gregos eram apenas o racionais. Isto é, números que podem ser escritos da forma p/q onde p e q são números inteiros. Esse conjunto numérico é simbolizado pela seguinte letra.

No entanto, foi dentre os pitagóricos (discípulos de pitágoras) que um infame número estranho, a um primeiro momento, surge. Esse número surge de um dos piares da escola pitagórica: o Teorema de Pitágoras. Em suma, o problema consiste em calcular a diagonal de um quadrado de lado 1, como da Figura 1.
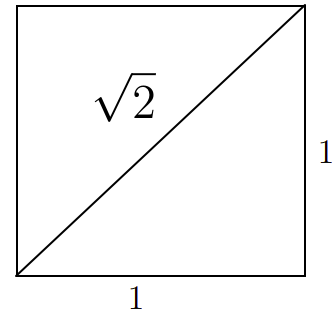
Hoje, com uma rápida aplicação do Teorema de Pitágoras podemos mostrar que a medida dessa diagonal é raiz 2. Todavia, esse cálculo, para essa época era inconcebível pois não havia-se como mensurar esse número raiz de 2. Logo, isso significaria que existem números além dos conhecidos, consequentemente, isso abalaria as estruturas do conhecimento dessa época.
Para se ter ideia, quando Hipaso (matemático grego responsável pelo problema), apresentou esse sugeriu que houvesse números além dos racionais sua vida foi rapidamente ceifada pelos pitagóricos. Sim, hipaso foi morto e logo jogado aos mares. Todavia, a matemática o faria justiça anos depois quando os homens entendessem a existência dos números irracionais.
Demonstrando que raiz de 2 é um número irracional
Agora que conhecemos o que são os números racionais e irracionais, podemos nos ater ao problema histórico que mencionei anteriormente. Nesse sentido, vamos mostrar que raiz de dois é um número irracional.
Para tanto, nós precisamos recorrer a uma técnica de demonstração específica chamada de redução ao absurdo. De fato, com essa técnica mostraremos que a suposição de que raiz de dois seja um número racional é um absurdo e inclusive contradiz noções matemáticas fundamentais. Dito isso, vamos fazer essa demonstração a seguir.

O tamanho dos Números racionais e irracionais
Agora, por fim, vamos falar sobre os tamanho do conjuntos dos racionais e do conjunto dos irracionais. De fato, quando falamos sobre tamanho de conjuntos de números é imediato pensarmos que esses conjuntos são infinitos. Todavia, quando nos atemos aos números irracionais há uma peculiaridade que aparece. De fato, há mais números irracionais do que números racionais.
Se gostou desse texto, confere também o artigo sobre números primos do Guru Nalbert.





