Fala gurunauta, nesse artigo vamos falar sobre o que são as transformadas de Laplace. Em geral, esse assunto aparece em cursos de cálculo avançado ou em equações diferenciais. No entanto, pode ficar tranquilo que hoje eu vou te explicar exatamente o que são as transformadas de Laplace e os principais tópicos do assunto para você mandar bem na sua prova.
Transformações lineares e a integral
Antes de começarmos a estudar nossas transformadas de laplace, vamos revisitar a ideia de uma transformação. De fato, em álgebra linear, somos apresentados a um conceito importante: as transformações lineares. Em suma, as transformações lineares (TL) são objetos parecidos com funções, todavia, elas associam vetores a outros vetores sob a condição de que a linearidade é mantida, isto é se T é uma TL e u,v vetores com a,b escalares vale que
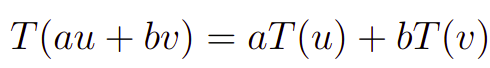
onde, a condição acima é chamada de linearidade. Nesse sentido, é interessante vermos que há diversos transformações lineares importante, por exemplo, a própria integral de fato, temos

onde f(x), g(x) são funções reais contínuas e a, b escalares. E lembre-se, da álgebra linear, conhecemos que funções são vetores definidas em espaços vetoriais específicos.
O ponto dessa discussão inicial é motivar você a uma rica teoria matemática: as transformadas integrais. Em particular, se você explorar a linearidade da integral é possível construir vários operadores lineares, além da transformada de Laplace, como por exemplo:
- A transformada de Fourier,
- Os operadores momento da mecânica quântica
- A transformada de Mellin.
Agora que você está motivado, vamos estudar as transformadas de Laplace.
Definição das transformadas de Laplace
Em primeiro lugar, vamos mostrar a definição da transformada de Laplace. Com efeito, está é
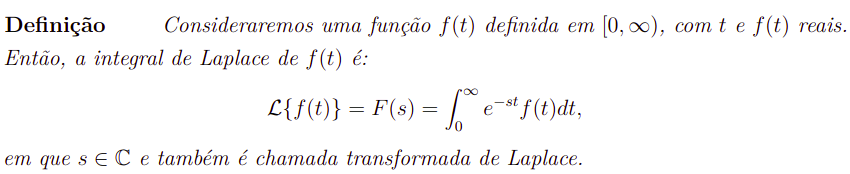
Ou seja, se você quiser calcular a transformada de Laplace de uma função f(t), você deve calcular a integral acima. Por exemplo, vamos calcular a transformada de Laplace da função f(t) = t com efeito

como você pode ver, em geral você deve apenas calcular uma integral e isso você já deve ter visto nos cursos introdutórios de cálculo. Além disso, vale citar que para o caso da função f(t) =t temos o importante resultado chamado de propriedade de translação da transformada de Laplace

Um ponto importante, é que você saiba que nem toda função terá transformada de Laplace. Decerto, basta você notar que em gera temos uma integral imprópria e, nem toda integral imprópria é convergente.
Tendo em vista que você, agora, conhece o que é a transformada de Laplace. Vamos citar algumas aplicações importantes, assim, você vai poder inclusive se convencer da força dessas transformadas.
Aplicações
Em termos gerais, a transformada de Laplace torna-se muito importante quando a empregamos em certos problemas matemáticos. Em particular, podemos citar dois
- Resolução de integrais impróprias,
- Solução de equações diferenciais.
Essas duas aplicações tornam esse assunto muito relevante. De fato, talvez você se pergunte por que isso é possível. A resposta para isso é simples: nós conhecemos as transformadas de Laplace.
Veja, quando eu digo que nós conhecemos, estou realmente dizendo que sabemos muito delas e até mesmo já calculamos muitas transformadas. Por conta disso, é possível encontrar diversas tabelas que contém a transformada de Laplace para diversas funções, tendo em vista isso veja a abaixo algumas dessas.
Tabela com as transformadas de Laplace importantes


Então, conhecendo os valores das integrais de Laplace já tabelados podemos ter resultados muito interessantes. Por exemplo, vamos calcular a seguinte integral imprópria

É gurunauta, nesse momento você vai ver que as técnicas usuais para o cálculo de integrais nos levariam a coisas muitos grandes. Porém se você consultar a figura 1, verá que a transformada de Laplace da função seno juntamente com a propriedade de translação é a seguinte

Logo, para s =1 na transformada de Laplace termos o seguinte:

assim, muito fácil e com poucas linhas de conta!. Com isso, você já pode ver a importância e força dessa transformada. Não vamos nos ater a como resolver equações diferenciais nesse artigo pois esse é um tópico que merece mais carinho e vamos fazer no futuro.
Mais um artigo ao fim gurunauta. Mas claro, eu tenho que te lembrar que, para todo perrengue universitário, a MeuGuru tem um guru especial para você. Conta com a gente que te ajudamos a salvar o semestre.





