O plano inclinado é um dos clássicos problemas físicos que aparecem desde o ensino médio até disciplinas do superior como Física 1 ou em mecânica newtoniana. No entanto, desde o ensino médio, problemas que envolvem planos e superfícies inclinadas geram confusões aos estudantes. Tendo isso em vista, nesse artigo, vamos esclarecer o plano inclinado, compreendendo-o e resolvendo um exemplo em apenas 4 passos.
1. Entendendo o plano inclinado
Primeiro de tudo, vamos buscar compreender o que é o plano inclinado. Esse objeto físico, é nada menos do que uma superfície que possui um certo declive, ou seja, uma inclinação em relação ao solo. Além disso, os problemas físicos que envolvem essas superfícies costumam, muitas vezes, abordar como seria o movimento de algum corpo que estivesse encima desse plano inclinado, por exemplo, como um bloquinho, de massa m, que deslizaria sobre ele como mostrado na Figura abaixo.

1.1 Entendendo o movimento bidimensional
Não apenas isso, mas um dos pontos que caracteriza e, gera várias dúvidas aos estudantes, é que: O movimento no plano inclinado ocorre em duas dimensões, ou seja, ele é bidimensional. De fato, se pensarmos que o bloco da Figura 1, começa a deslizar-se, então, ele vai estar se movendo tanto para a esquerda como, também, para baixo. Assim, ocorrendo em duas dimensões.
3. Montando o diagrama de forças
Agora que entendemos o que de fato é o plano inclinado, resolveremos esse problema com as leis de Newton. A primeira coisa que devemos ter em mente, é que devemos visualizar o problema com as leis de Newton, assim, escreveremos todas as forças que atuam sobre esse bloco conforme mostrado na Figura 2.
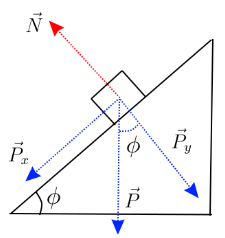
3.1 Entendendo as forças
Em que, as forças que aparecem na Figura 2, são:
- A força peso, que denotamos com a letra P maiúscula,
- A força normal, que denotamos com a letra N maiúscula.
Além disso, há ainda as forças que vamos chamar de Px e Py. Essas, na verdade, fazem parte da força peso, mas como o movimento do bloco ao longo do plano inclinado acontece em duas dimensões, logo a força peso aparece inclinada e, então, se decompõe em duas outras forças, uma para cada dimensão do movimento.
Com isso, resta a entendermos como as forças mostradas na Figura 2, se relacionam. Para isso, façamos uma sutil mudança de ponto de vista, conforme mostrado na Figura 3.
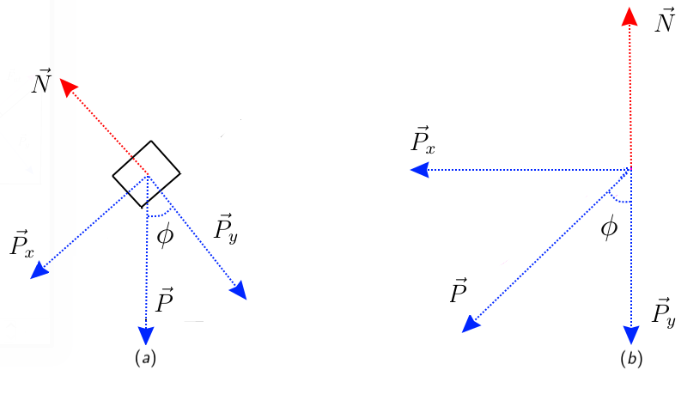
3.2 Escrevendo as equações
Decerto, a figura 3 (b) apresenta a nós, uma forma convencional de vermos as forças que atuam no bloco do plano inclinado. Com isso, descrever como as forças peso e normal agem sobre o bloco torna-se fácil, assim, primeiramente, vamos decompor a força peso que, com uso das relações trigonométricas , obtemos as seguintes equações:

Então, usando as leis de Newton, conseguimos, enfim, escrever uma expressão para as acelerações de ambos os eixos. Basta ver que no eixo x, a única força existente deve ser a decomposição da força peso em x, enquanto que, no eixo y temos uma subtração de forças, sendo essas da componente da força peso em y e da normal como mostrado na Figura 3. Assim, usando a segunda lei de Newton, obtermos as seguintes equações de movimento.

Com isso, obtemos a descrição da dinâmica de um bloco sobre o plano inclinado e estamos aptos para resolver quaisquer problemas, basta empregarmos as duas equações acima que obtivemos.





