Nesse texto, vamos ver o que é um Polinômio de Taylor. Hoje nós da MeuGuru preparamos um artigo especial para você sobre um dos temas que causam grande terror nas cadeiras de Cálculo. De fato, quando começamos a falar sobre derivadas vemos que, obter a derivada de uma função é um processo aproximativo. Não apenas isso, mas esse processo, por meio do limite, permite uma aproximação muito boa para a inclinação da reta tangente num ponto avaliado da curva.
Todavia, esse processo considera apenas um desvio linear. Consequentemente, há vários termos que acabam por ficar ocultos nesse processo. Mas, para certas funções é necessários considerá-los. Tendo isso em vista, os polinômios de Taylor são uma forte ferramenta matemática, analítica e numérica para isso. Então, vem comigo e vamos juntos conhecer a beleza desses polinômios.
Motivação para o Polinômios de Taylor
Bom de início, vamos revisitar a ideia das derivadas. Com efeito, consideremos uma função f(x) com efeito, a equação da reta tangente a f(x) num ponto a do seu domínio é

Em suma, temos que apenas a derivada primeira f'(a) aparece na Expressão 1. Em geral, isso é mais do que o suficiente para você ter uma boa aproximação. Entretanto, a medida que conseguimos obter uma reta tangente somos motivados a pensar o seguinte.
“Seria possível, aproximarmos cada vez mais e de forma melhor as retas tangentes por funções polinomiais até que elas fossem essencialmente similares a curva f(x) ?”
E a resposta é sim gurunauta. Então, é com essa premissa que vamos introduzir os polinômios de Taylor.
Polinômio de Taylor de grau n
Em verdade, o obtenção de uma aproximação em polinômios para uma função f(x) diferenciável é feita melhorando a Expressão 1, o que pode ser feito, inicialmente, incluindo a derivada segunda na Expressão 1 da seguinte forma
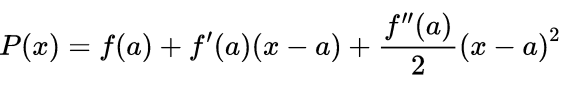
Decerto, a Expressão 2 melhora a aproximação da Expressão 1 para valores de x próximos ao valor x=a. Em particular, essa expressão é o chamado polinômio de Taylor de grau 2, pois considera desvios apenas até o termo quadrático.
Todavia, podemos generalizar a ideia a expressão 2. Para isso, tendo em mãos a condição de que f(x) é n vezes diferenciável podemos evocar o polinômio de Taylor de grau n, o qual é dado a seguir.
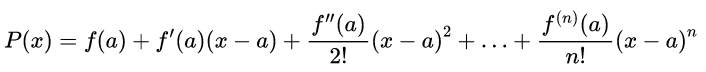
Com isso em mãos, é possível aproximar-se suficientemente bem uma função f(x) com as hipóteses acima em torno do ponto x=a.
Note ainda que, os termos do polinômio de Taylor podem ser agrupados num somatório sob a expressão de um termo geral, que é o seguinte
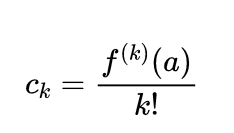
aqui o índice (k) da função f denota a derivada k-ésima. Com isso, obtem-se a seguinte expressão para o Polinômio de Taylor
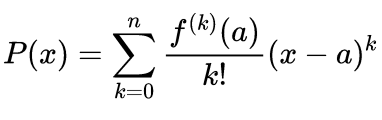
As Expressões 5 e 3 são equivalentes gurunauta, escolha a que você se sentir melhor para usar, o importante é que você aprenda e domine o conteúdo.
Observação sobre o centro x=a do polinômio de Taylor
O processo obtido pelo polinômio de Taylor é fantástico. Em verdade, com ele muitas cálculos na engenharia e até mesmo na astrofísica de buracos negros torna-se possível. Todavia, ele se baseia na ideia de derivada, portanto, é um processo Local. Ou seja, quando escolhemos o centro x=a nosso polinômio será na verdade uma aproximação da função em torno do ponto x=a. Nem sempre será possível ter uma aproximação com esses polinômios para todo x do domínio da função f(x).
Exemplo resolvido
Agora, vamos resolver um problema. Vamos determinar o polinômio de Taylor de grau 4 para a função cosseno de x centrada em a=0. Com efeito, nosso polinômio pela expressão 3 e/ou 5 é o seguinte:

Nosso trabalho aqui gurunauta será, na maioria esmagadora das vezes, determinar os as derivadas da função f(x)=cos(x) até a ordem do polinômio pedido. Nesse sentido, teremos o seguinte passo a passo

Com isso em mãos, fica fácil ter o resultado desejado. Com efeito, basta substituir cada termo acima na expressão anterior, de fato teremos

que é o polinômio, para a função f(x)=cos(x) para x centrado em a=0.
Com isso, chegamos ao fim gurunauta. Aliás, preciso de contar uma coisa importante. Esse artigo é introdutório beleza? nossa ideia é abordar em linhas gerais o polinômio de Taylor. Em verdade, esse assunto possui diversos outros fundamentos teóricos que não abordamos aqui, a citar o resto de Lagrange e como garantir a convergência dos termos. Então, fica atento gurunauta que logo logo vamos ter uma parte 2 desse texto, mete bronca guru salve aluno!.
