Neste post, você aprenderá sobre o funcionamento e a operacionalização dos cálculos referentes ao Sistema de Amortização Francês (Tabela PRICE).

Olá pessoal! Trago hoje um resumo sobre outro assunto visto como complicado dentro da disciplina de Matemática Financeira: SISTEMAS DE AMORTIZAÇÃO, mais precisamente a respeito do Sistema de Amortização Francês (Tabela Price).
Espero que este material auxilie o estudo de vocês! 😉
# INTRODUÇÃO
De modo simplificado, podemos entender que “amortizar” significa pagar gradual ou parcialmente alguma dívida, abatendo parte do valor total devido. Assim, os sistemas de amortização existentes representam diferentes formas de se pagar uma determinada dívida.
Seja qual for o sistema de amortização, iremos trabalhar com alguns elementos essenciais que compõem o processo em questão, a saber: prestação, amortização, juros, saldo devedor, taxa e prazo, cujos conceitos já foram abordados na publicação disponível clicando AQUI!
Bem, a depender de como essas variáveis se comportam ao longo do financiamento, existem basicamente cinco sistemas de amortização principais no mercado financeiro, a saber:
- Sistema de Amortização Constante (SAC);
- Sistema de Amortização Francês (PRICE);
- Sistema de Amortização Misto (SAM);
- Sistema de Amortização Americano (SAA); e
- Sistema Bullet.
Portanto, hoje, aprenderemos especificamente sobre o sistema de amortização francês.
# O SISTEMA DE AMORTIZAÇÃO FRANCÊS (PRICE):
O Sistema de Amortização Francês (também conhecido por Tabela Price ou simplesmente Price, em virtude do sobrenome de seu criador) é caracterizado por possuir PRESTAÇÕES com valor constante. Mas, você notou a diferença?! No sistema SAC, a Amortização é constante; no sistema PRICE, a Prestação é constante!
*ATENÇÃO: não é o valor da amortização que é fixo, mas sim o valor da prestação (P) é que se mantêm constante ao longo de todo o prazo do financiamento! O valor da amortização (A) é crescente e, consequentemente, os juros (J) são decrescentes, pois a taxa (i) incide sobre um saldo devedor cada vez menor.
Assim sendo, estamos diante de um sistema que trabalha com as chamadas SÉRIES PERIÓDICAS UNIFORMES (ou Rendas Certas, Anuidades, entre outros sinônimos), que nada mais é que uma situação em que um mesmo fluxo se repete em períodos uniformes ao longo do tempo.
Portanto, para calcular o valor da PARCELA no Sistema de Amortização Francês, basta utilizar a fórmula de séries periódicas uniformes (onde VP é o valor presente da dívida, P é a prestação, i é a taxa de juros e n é a quantidade de períodos da operação):
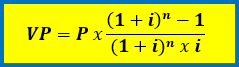
Contudo, você também pode trabalhar com uma versão reestruturada dessa fórmula anterior (ambas possuem a mesma finalidade e resultam exatamente no mesmo valor, sendo apenas formas diferentes de estruturação da conta), conforme abaixo:

Então, utilizando como exemplo o financiamento hipotético de R$ 100.000,00, em 5 parcelas mensais, a uma taxa de 2% a.m., teríamos a seguinte prestação no sistema Francês:
R$ 100.000,00 = P x [(1 + 2%)5 – 1] / [(1 + 2%)5 x 2%]
Portanto, tem-se: R$ 100.000,00 = P x 0,1040808 / 0,0220816
R$ 100.000,00 = P x 4,71346
P = R$ 100.000,00 / 4,71346
P = R$ 21.215,84
Portanto, cada uma das cinco prestações será sempre de R$ 21.215,84 ao mês, valor este que engloba a amortização e o juros do período
Então, sabendo o valor da parcela mensal, podemos ver como esse sistema se comporta ao longo de todo o financiamento, conforme sintetizado no quadro a seguir:
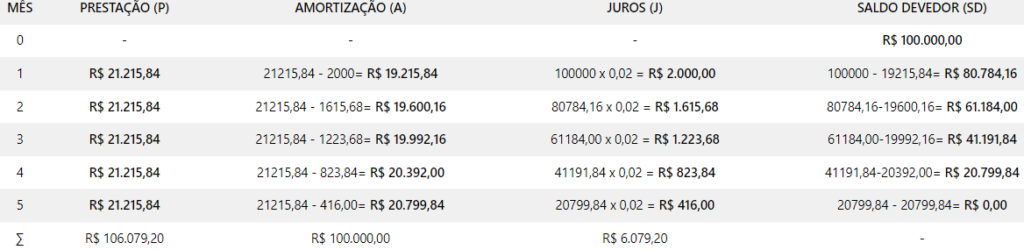
Gaste um tempo aqui para analisar todos os campos da tabela acima, sem pressa! Procure entender cada detalhe!
Perceba que o valor de cada prestação, mesmo constante, portanto, continua sempre sendo igual à soma da amortização com os juros do respectivo período.
Além disso, a soma de todas as amortizações equivale ao saldo devedor original (R$ 100.000,00), liquidando a dívida após a última parcela. E, como já mencionado, o valor dos juros (J) de cada período decresce ao longo do tempo, enquanto a amortização (A) aumenta mês após mês.
Mas, outra observação interessante para resolução de questões é que, no Sistema Francês, a amortização cresce a uma taxa de (1+i) ao período. Em outros termos, An-1 x (1 + i)= An. No caso em análise, esse crescimento pode ser demonstrado, por exemplo, da seguinte forma: A1 x (1 + i) = A2 –> R$ 19.215,84 x 1,02 = R$ 19.600,16.
Essa característica é valiosa para facilitar a resolução de alguns exercícios! 😉
# CONCLUSÃO:
Por fim, vale destacar que alguns detalhes adicionais podem surgir, a depender da forma como se dá o pagamento da dívida.
Alguns financiamentos exigem o pagamento de uma entrada, por exemplo. Também é possível que um período de carência seja concedido antes do início das prestações, ou seja, um prazo inicial de “respiro”, sem qualquer pagamento, o que demandará ajustes pontuais na resolução, por representar uma série periódica DIFERIDA.
Por outro lado, pode acontecer de a primeira parcela ser paga no ato da compra, já abatendo na data zero esse valor do saldo devedor inicial, o que caracteriza a chamada série periódica ANTECIPADA. Mas, fique tranquilo, pois veremos todas essas e outras variações de cobrança do conteúdo!!
Então, é isso! No post de hoje, vimos apenas o sistema de amortização francês. Os demais estão abordados nos seguintes posts: SAC, SAM, SAA e Bullet.
Chega por hoje, pessoal! 😉
Para maiores esclarecimentos e aprofundamento na disciplina de Matemática Financeira, continuem me acompanhando aqui no blog da Meuguru!

Até o próximo post!
Prof. Rodrigo Xavier
