
E aí, gurunautas, tudo bem? No último post, estudamos um pouquinho (bem pouquinho mesmo) sobre Programação, Linguagem de programação e Python, então, hoje vamos dar continuidade no assunto.
Python: Operações Aritméticas
Primeiramente, precisamos definir algumas coisinhas, no Python, as operações aritméticas são fundamentais e assim como em qualquer calculadora gráfica e incluem adição, subtração, multiplicação, divisão e exponenciação. Nesse sentido, temos alguns operadores aritméticos que representados por símbolos específicos: + para adição, – para subtração, * para multiplicação, / para divisão e ** ou pow() para potências. A linguagem reserva esses símbolos para indicar as operações correspondentes, o que facilita a execução de cálculos de forma prática e direta, sem causar confusão com outros tipos de variáveis, como strings.
Apenas para exemplificar, ao realizar uma operação de adição, você simplesmente usa o operador + entre dois números, como em 3 + 2, e o Python resolve a operação. Essa lógica aplica-se igualmente a outras operações, permitindo execução de cálculos de forma bem ampla, lembre-se, cada linguagem tem sua característica, em algumas a potência é ^, então, cuidado.
A ordem de operações
A ordem de operações define uma sequência padrão para a execução de diferentes cálculos, isso é na vida, a ordem de operação vem da aritmética. No Python, essa ordem segue as mesmas regras que você aprendeu na escola, garantindo previsibilidade nos resultados. Primeiramente, são realizadas as potências, seguidas pela multiplicação e divisão, e, por fim, pela adição e subtração.
Além disso, o uso de parênteses permite alterar essa sequência padrão. Por exemplo, na expressão 2 + 3 * 4, executa-se a multiplicação antes da adição. Porém, se você usar parênteses, como em (2 + 3) * 4, a adição vem primeiro, alterando o resultado para 20, tal qual o que a matemática ordena. Nada novo por aqui! Porém, isso permite, em termos de algoritmos, controlar precisamente como executar as operações, o que é útil em cálculos complexos ou fórmulas extensas.
Módulo Math
O Python oferece uma ampla gama de funções aritméticas básicas para facilitar cálculos matemáticos. Entre elas estão sin, cos, tan (funções trigonométricas), asin, acos, atan (funções trigonométricas inversas), exp (exponencial), log (logaritmo natural), log10 (logaritmo na base 10) e sqrt (raiz quadrada). O módulo chamado math armazena essas funções, e você precisa importá-lo antes de utilizá-las.
E é fácil, para acessar, basta usar o comando import math no início do código. Após isso, você pode chamar as funções diretamente, como em math.sqrt(16) para calcular a raiz quadrada de 16. Essa abordagem modular permite que o Python seja eficiente e organizado, carregando somente os recursos necessários para cada aplicação. Bizu importante: ao fazer import math as m, assim math.sqrt(16) se torna m.sqrt(16).
Estrutura de Repetição “for-loops”
Um for-loop é uma estrutura que permite repetir um conjunto de instruções para cada valor presente em uma sequência. Chamamos esse tipo de loop de “loop definido” porque a sequência fornecida determina um início e fim predefinidos. Embora existam outros tipos de loops, abordaremos esses em outra oportunidade.
A sintaxe geral de um for-loop no Python é:
for variável in sequência: # instruções a serem executadas
Aqui, o Python percorre cada item da sequência, atribuindo-o à variável especificada, e executa as instruções dentro do bloco do loop. Por exemplo:
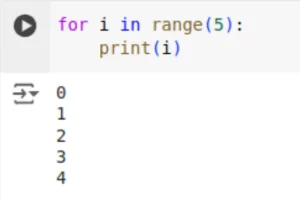
Esse código imprime os números de 0 a 4, um por linha, pois a função range(5) gera uma sequência de 0 a 4. Essa estrutura é muito utilizada para resolver problemas que envolvem iteração.
Além disso, no for-loop, o processo inicia atribuindo o primeiro elemento da sequência à variável de loop. Em seguida, todas as instruções do bloco de código são executadas. Uma vez que, após essa execução, o loop passa ao próximo elemento da sequência, repete o bloco de código, e assim por diante.
Dessa maneira, esse ciclo de atribuição e execução continua até que todos os elementos da sequência sejam processados. Quando não há mais elementos disponíveis, o loop é encerrado automaticamente.
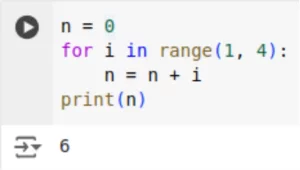
Nos exemplos mostrados temos:
- Na primeira iteração, i recebe o valor do range(5), [0,1,2,3,4] e os imprime, um por vez.
- Na segunda iteração, número é atualizado para 2, e assim por diante e imprime o resultado (6).
Esse comportamento torna o for-loop eficiente para percorrer qualquer coleção de dados, como listas (com strings) ou intervalos. Porém, o que discutimos até aqui é o suficiente para implementarmos um algoritmo e resolver um problema clássico de Cálculo Numérico, que são as integrações numérica.
Integração numérica
Mas o que é integração numérica? Calma, meu bom! Para aproximar a integral de uma função f(x) no intervalo [a,b], utilizamos um método de discretização. E aí? Traduzindo dividimos o intervalo total em uma grade numérica de n+1 pontos, com espaçamento h=nb−a. Assim, xi denota cada ponto na grande, em que x0=ae xn=b.
A contagem dos pontos começa em x0, resultando em n+1 pontos no total. Chamamos de subintervalo o intervalo entre dois pontos consecutivos, xi,xi+1. Dessa maneira, assumimos que avalia-se a função f(x) em qualquer ponto da grade ou que seus valores nos pontos xisão. Utilizamos métodos como a regra do trapézio, integração de Riemann e Simpson para obter a aproximação dessa integral.
Não iremos abordar todas as regras agora, nesse post iremos falar apenas da Regra de Simpson.
Regra de Simpson no Python
Podemos usar a Regra de Simpson para aproximar a integral de uma função f(x) sobre o intervalo total [a,b]. O método envolve somar as contribuições das áreas aproximadas por polinômios quadráticos Pix ajustados a cada par de subintervalos consecutivos.
Para cada dois subintervalos [xi−1, xi] e [xi, xi+1] , a integral aproximada é:
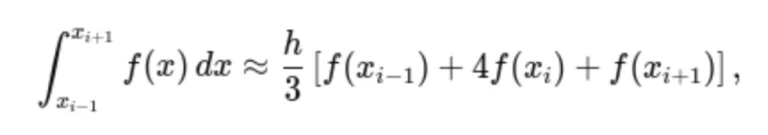
sendo que h é o espaçamento entre os pontos xi−1, xi e xi+1. Porém, se quisermos para n subintervalos (não apenas n =3) a nossa formulinha fica assim:
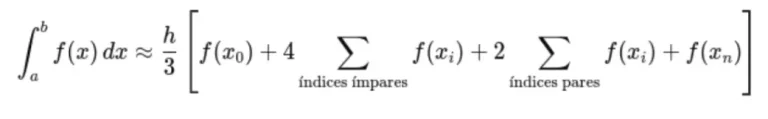
Não vou lhe assustar para mostrar de onde tiramos isso, mas é simples, é de uma interpolação lagrangeana para múltiplo de 3.
Para aplicar corretamente a Regra de Simpson
É necessário ter um número par de subintervalos, o que implica que o número de pontos na grade seja ímpar. Isso ocorre porque a regra ajusta um polinômio quadrático a cada par de subintervalos consecutivos [xi−1,xi] e [xi,xi+1]. De um jeito mais simples, se eu vou ajustar a um polinômio quadrático, preciso de no mínimo 3 pontos, então a cada subintervalo, estou ajustando a um polinômio de grau 2. Pegou? É isso aí! Vamos continuar!
Para que isso funcione, a grade precisa ter exatamente um número ímpar de pontos, garantindo que cada par de subintervalos seja bem definido. Note na imagem, que a fórmula da Regra de Simpson pode ser aplicada corretamente porque o número de pontos é ímpar (9 pontos), permitindo que as integrais sobre os subintervalos consecutivos sejam somadas, note também, o quanto é importante a escolha adequada da malha para um melhor aproximação.
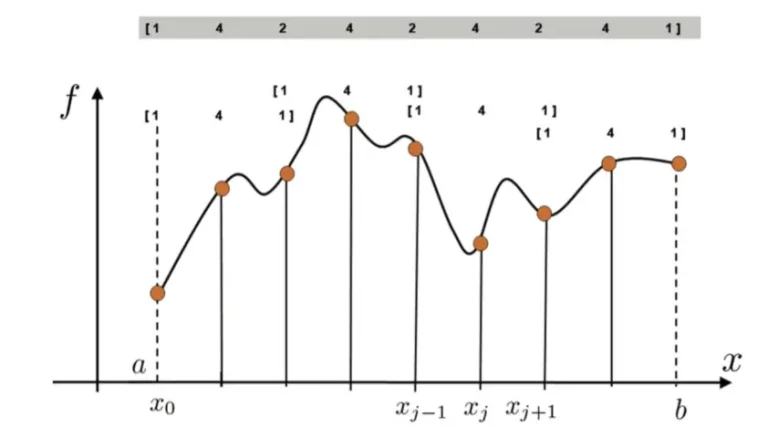
O que definimos aqui, é conhecido também como 1/3 de Simpsons, porém, a Regra de Simpson 3/8 é uma variação que utiliza um polinômio cúbico para aproximar a integral de uma função, sendo uma alternativa à Regra 1/3 de Simpson quando o intervalo é dividido em múltiplos 3, porém n par. Mas vamos logo ao que diz o título do post, resolver uma atividade.
Python: Resolvendo uma atividade de Cálculo Numérico
Usando a 1/3 de Simpsons, encontrar uma aproximação para a integral definida da função f(x) 16−x2, no intervalo [-4, 4], o algoritmo abaixo utiliza a função, porém, preciso informar quantos subintervalos eu quero (n = 16) então ele irá calcular os valores de xi e de yie então aplicar a formulação, porém, o algoritmo pode ser, facilmente, ajustado para utilizar os vetores xi e yi.
Assim,
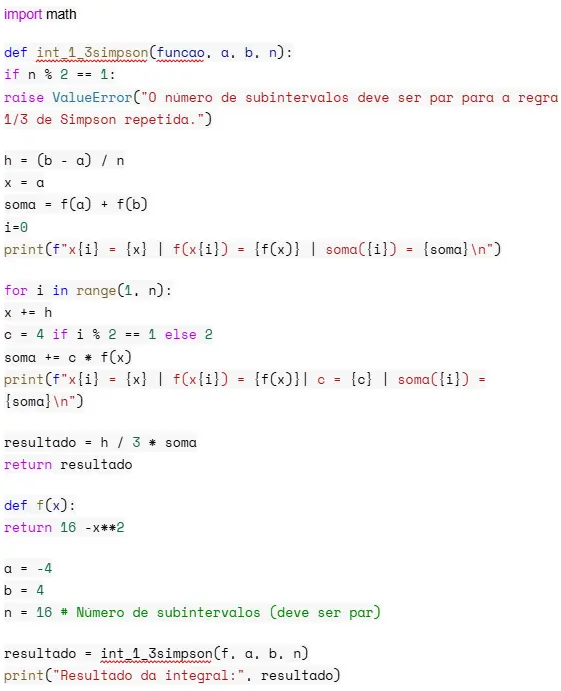
Temos a saída:
x0 = -4 | f(x0) = 0 | soma(0) = 0
x1 = -3.5 | f(x1) = 3.75| c = 4 | soma(1) = 15.0
x2 = -3.0 | f(x2) = 7.0| c = 2 | soma(2) = 29.0
x3 = -2.5 | f(x3) = 9.75| c = 4 | soma(3) = 68.0
x4 = -2.0 | f(x4) = 12.0| c = 2 | soma(4) = 92.0
x5 = -1.5 | f(x5) = 13.75| c = 4 | soma(5) = 147.0
x6 = -1.0 | f(x6) = 15.0| c = 2 | soma(6) = 177.0
x7 = -0.5 | f(x7) = 15.75| c = 4 | soma(7) = 240.0
x8 = 0.0 | f(x8) = 16.0| c = 2 | soma(8) = 272.0
x9 = 0.5 | f(x9) = 15.75| c = 4 | soma(9) = 335.0
x10 = 1.0 | f(x10) = 15.0| c = 2 | soma(10) = 365.0
x11 = 1.5 | f(x11) = 13.75| c = 4 | soma(11) = 420.0
x12 = 2.0 | f(x12) = 12.0| c = 2 | soma(12) = 444.0
x13 = 2.5 | f(x13) = 9.75| c = 4 | soma(13) = 483.0
x14 = 3.0 | f(x14) = 7.0| c = 2 | soma(14) = 497.0
x15 = 3.5 | f(x15) = 3.75| c = 4 | soma(15) = 512.0
Resultado da integral: 85.33333333333333
Se quiser, pode alterar e brincar modificando a função e n intervalos.
Até a próxima!
Veja mais em nosso blog:





