
Hoje nosso texto é sobre Regras de Trapézio! Você já se perguntou como calcular as antiderivadas de funções que não podem ser expressas de maneira simples ou em termos de funções conhecidas? Pois bem, nesses casos, torna-se impossível calcular diretamente suas integrais definidas. Por isso, precisamos buscar alternativas que resolvam esse problema, e uma das soluções mais úteis é a integração numérica. Esse método permite aproximar os valores das integrais utilizando abordagens específicas.
Entre os métodos mais comuns estão o método do trapézio e o método de Simpson, que dividem a área sob a curva em formas geométricas mais simples e fáceis de calcular. Entretanto, cada método apresenta vantagens e desvantagens, dependendo da função, do intervalo de integração, do objetivo e da precisão desejada.
Métodos de Aproximação e Estimativa de Erro
Para começar, o método do trapézio aproxima a área sob a curva utilizando segmentos de linha reta que conectam pontos consecutivos (formando trapézios). De maneira geral, essa abordagem é simples e funciona muito bem para funções com comportamentos mais lineares. Além disso, sua precisão depende diretamente da quantidade de subconjuntos nos quais os dados são divididos. No entanto, ele pode ser impreciso para funções com comportamentos mais complexos.
Por outro lado, o método de Simpson utiliza parábolas para aproximar os segmentos da curva. Embora seja um pouco mais complexo, ele tende a ser mais preciso do que o método do trapézio. Assim, a escolha entre os métodos depende dos objetivos do cálculo e do nível de precisão desejado. Ademais, é fundamental avaliar o erro da integração para compreender o quão próximo o resultado está do valor real. Métodos analíticos e empíricos podem ajudar nessa estimativa. Mas calma, vamos abordar tudo passo a passo!
Regras de Trapézio
Como o próprio nome sugere, vamos calcular a área (ou integral) utilizando trapézios. Para isso, é importante visualizar bem o conceito. Observe atentamente a imagem e perceba como os trapézios se ajustam sob a curva para fornecer uma estimativa da área.
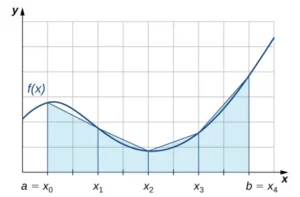
A regra trapezoidal utiliza trapézios para estimar integrais definidas, proporcionando uma aproximação mais eficiente da área sob uma curva. Essa técnica se baseia na divisão do intervalo de integração em subintervalos iguais, cada um representado por um trapézio. O comprimento de cada subintervalo é denotado por Δx, sendo essencial para calcular a área aproximada.
Para entender a forma final da regra trapezoidal, considere os trapézios apresentados na imagem anterior. A fórmula básica da área de um trapézio com altura h e bases paralelas de comprimentos b1 e b2, a área será A= ½ h (b1 + b2). Aplicando esse conceito, o primeiro trapézio tem uma altura Δx e bases paralelas com valores correspondentes às funções f(x0) e f(x1). Assim, a área desse trapézio pode ser representada como A1 = ½ Δx (f (x0) + f(x1)).
As áreas dos três trapézios restantes são
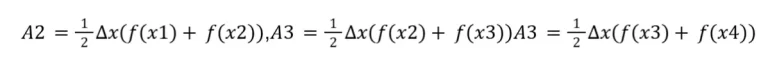
Assim, veja bem
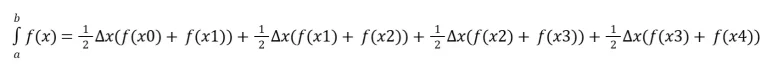
Note, algo muito importante, vamos colocar em evidência:
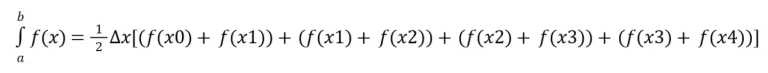
Viu algo interessante? Não? Vou falar, observe que o fx0 e fx4os outros valores estão duplicados! Então vamos reescrever:
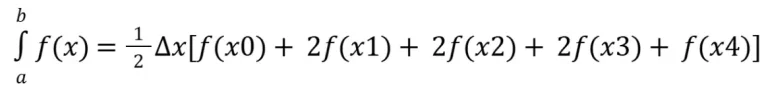
Calma, estamos quase lá, quanto maior a quantidade de subintervalos, melhor será a aproximação, e a fórmula acima, que desenvolvemos pode ser generalizada para xn, como? Simples, fazemos: Δ𝑥 = 𝑏−𝑎 / 𝑛 então podemos reescrever (afinal, entre x0 e xn, vamos ter “valores duplicados”):
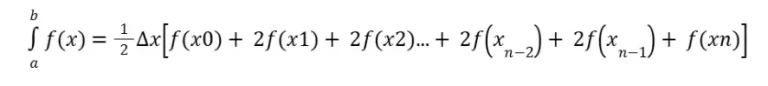
Difícil? Claro que não, No caso mais básico (Trapézio Simples), quando n=1, toda a curva é aproximada por um único trapézio, o que funciona bem para funções lineares, mas pode introduzir erros significativos em funções mais complexas ou curvas acentuadas. O que desenvolvemos aqui, é o Trapézio Repetido.
Quando queremos melhorar a precisão, aumentamos o número de divisões (n), o que significa dividir o intervalo em partes iguais e calcular a soma das áreas de múltiplos trapézios. Importante: o intervalo x deve ser dividido de forma constante, ou seja, as larguras (Δx) devem ser iguais. Se os subintervalos não forem equivalentes (divisão irregular), ainda é possível aplicar o Método do Trapézio, mas será necessário calcular cada área separadamente (por exemplo A1, A2, A3 ,…), como fizemos logo no início.
Exercício de Aplicação com relação às Regras de Trapézio
Use a regra do trapézio para estimar ¹∫₀ x² dx usando quatro subintervalos.
Os extremos dos subintervalos consistem nos elementos do conjunto P = 0, ¼, ½, ¾, 1 e
Δx = (1−0) / 4 = ¼
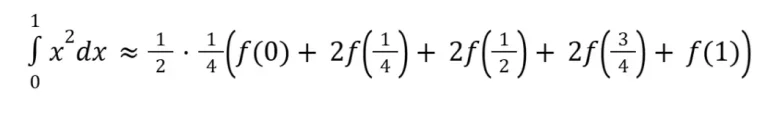
aplicando os valores
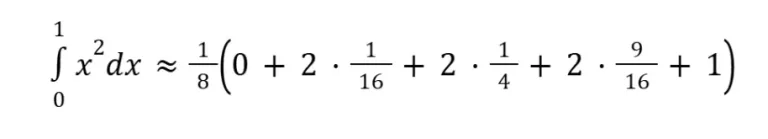
e assim, temos
¹∫₀ x² dx ≈ 11/32
Muito simples, certo? Mas antes de finalizarmos, vamos dar uma olhada no erro. Lembra que eu comentei? Afinal, é importante avaliar se a aproximação será válida para a aplicação e se o erro é aceitável.
Limites de erro para as regras de trapézio
Seja f(x) uma função contínua no intervalo [a,b], que possui uma segunda derivada f′′(x) sobre este intervalo. Se M é o valor máximo de ∣f′′(x)∣ no intervalo [a,b], então os limites superiores para o erro ao usar Mn e Tn para estimar ᵇ∫ₐ f (x) dx são:
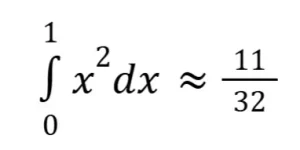
Note que só é possível calcular esse limitante, se o modelo f(x) for conhecido! Utilizar derivadas numéricas para encontrar o M acaba se tornando computacionalmente muito exigente e menos preciso. Ufa, apesar de existir outros métodos, faremos isso em outra oportunidade!
Veja mais em nosso blog
Movimento Circular Uniforme: Como funciona a Física por trás?
Direitos Sociais: Evolução Histórica e o Estado de Bem-Estar





