O Teorema do Núcleo e da Imagem é um dos resultados mais importantes vistos num primeiro curso de Álgebra Linear. De fato, o estudo de transformações lineares corresponde a boa parte da carga horária desse curso, o que se justifica frente a relevância do assunto tanto como base para outras áreas da matemática como também em vista das diversas aplicabilidades existentes nas ciências físicas e aplicadas.
Nesse sentido, o Teorema do Núcleo e da Imagem aparece como um importante resultado que caracteriza a dimensão de transformações lineares, de seus núcleos e de suas imagens. Portanto, esse resultado matemático é de suma importância ao passo que fornece informações relevantes sobre o objeto mais importante da álgebra linear: as transformações lineares.
Então, hoje nós da Meu Guru trouxemos esse importante texto para você Gurunauta. Com efeito, nesse texto faremos um tutorial rápido, preciso e objetivo sobre o que é o Teorema do Núcleo e da Imagem. De fato, vamos te mostrar como você deve usá-lo ao tanto para caracterizar transformações lineares quanto a serem ou não um isomorfismo como também como você pode determinar dimensões dos conjuntos do núcleo da transformação linear.
O que é o Teorema do Núcleo e da Imagem
Certamente, é importante entendermos o que de fato é esse Teorema que estamos nos referindo tanto. Nesse sentido, é válido nos adentrarmos ao entendimentos dos Teoremas do Núcleo e o da Imagem os quais quando combinados nos permitem obter a relação desejada que fixa o Teorema do Núcleo e da Imagem. Com efeito, vamos então conhecer um pouco desses resultados.
De início, vamos ao Teorema do Núcleo, também conhecido como Teorema do Núcleo-Nulidade, estabelece uma relação entre o núcleo (ou kernel) de uma transformação linear e a sua dimensão. Em suma, o núcleo de uma transformação linear é o conjunto de vetores de entrada que são mapeados para o vetor nulo. Então, o Teorema do Núcleo afirma que a dimensão do núcleo é igual à diferença entre a dimensão do espaço de partida e a dimensão do espaço de chegada.
Por outro lado, o Teorema da Imagem, também conhecido como Teorema da Imagem-Posto, estabelece uma relação entre a imagem de uma transformação linear e a sua dimensão. Com efeito, a imagem de uma transformação linear é o conjunto de todos os vetores de chegada que são efetivamente alcançados pela transformação. Então, o Teorema da Imagem afirma que a dimensão da imagem é igual ao posto da transformação, que é o número máximo de vetores linearmente independentes na imagem.
Então, tanto o Teorema do Núcleo quanto o Teorema da Imagem fornecem uma visão abrangente sobre as propriedades das transformações lineares. Portanto, ao combinarmos esses teoremas somos capazes de compreender a estrutura e a dimensionalidade das transformações lineares, sendo ferramentas indispensáveis para análises e aplicações em diversos campos, como álgebra, análise funcional, equações diferenciais, processamento de sinais e aprendizado de máquina.
Enunciado do Teorema do Núcleo e da Imagem
Então, vamos agora ao enunciado do Teorema do Núcleo e da Imagem. Decerto, aqui não estamos interessados em sermos rigorosos e profundos em nossa abordagem. Com efeito, nosso objetivo é simplesmente te apresentar o essencial que te permitirá arrasar na sua prova e fugir das provas finais. Dito isso, vamos ao que interessa, vamos considerar uma Transformação linear T: V->U onde V e U são dois espaços vetoriais de dimensão finita. Sob essas condições vale as seguintes igualdades
dim(V) = dim(ker(T)) + dim(Im(T)) = null(T) + rank(T)
onde dim(W) denota a dimensão do espaço vetorial W, e ker(), Im(), null() e rank() denotam, respectivamente o Kernel, a Imagem, a nulidade e o rank do argumento do parênteses (). Decerto, esses conceitos foram abordados no artigo 2 da série de álgebra linear. Ademais, recomendamos fortemente que você veja esse artigo visto que lá temos um exemplo resolvido passo a passo sobre o assunto.
Transformações injetivas, sobrejetivas e bijetivas
Agora, de posse do conhecimento do Teorema do Núcleo e da Imagem podemos então caracterizar uma transformação linear quanto a sua injetividade, sobrejetividade e ainda sobre a bijetividade.
Primeiramente, uma transformação linear T:V->U é dita injetiva se e somente se a dimensão do seu núcleo for 0. Ou seja, uma correspondência linear T para ser injetiva requer que o único vetor em seu núcleo seja o vetor nulo.
Por outro lado, dizemos que uma transformação T:V->U é sobrejetiva se e somente se a transformação T for capaz de produzir todos os elementos U a partir dos elementos de V.
Por fim, dizemos que uma transformação linear T:V->U é bijetiva se e somente se ela for uma transformação injetiva e sobrejetiva. Ademais, quando uma transformação T:V->U for bijetora dizemos que ela é um isomorfismo.
A relação com o Teorema do Núcleo e da Imagem
Com efeito, é claro que essas definições aparecem intimamente ligadas as noções de dimensões dos espaços vetoriais considerados pela transformação T. Assim, nem tenha dúvidas que muitas questões de álgebra linear das suas listas e quiça das suas provas serão associadas a determinação da injetividade/sobrejetividade de uma transformação linear a partir do entendimento do seu núcleo e afins.
Nesse sentido, vamos no exemplo a seguir estabelecer uma solução de um exercício que fará com que todos esses assuntos fiquem relacionados e poderá a te ajudar bastante a entender como você deve pensar para responder essas questões.
Um exemplo resolvido passo a passo
Então, vamos resolver um problema associado a uma transformação linear T. Com efeito, consideremos a transformação linear T: M2×2-> R dada por:
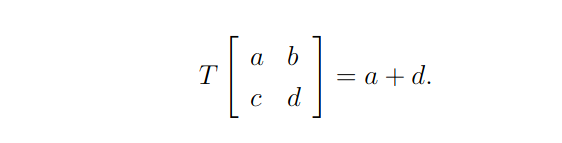
De posse disso, vamos determinar o núcleo da transformação que é feito do seguinte modo:
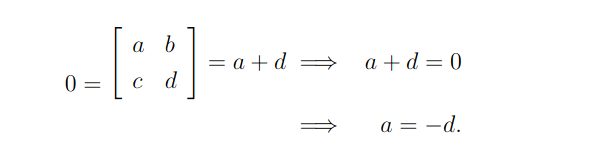
logo todas as matrizes 2×2 cujo condição em que a = -d seja satisfeita estarão no núcleo de T. Logo, as matrizes devem ter a seguinte forma:
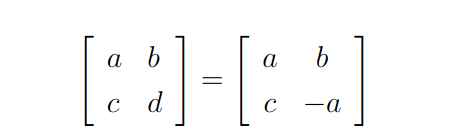
A partir da forma geral desse vetor vamos obter a quantidade de vetores que formam a base do núcleo de T. Para isso, veja que devemos fazer o seguinte procedimento:
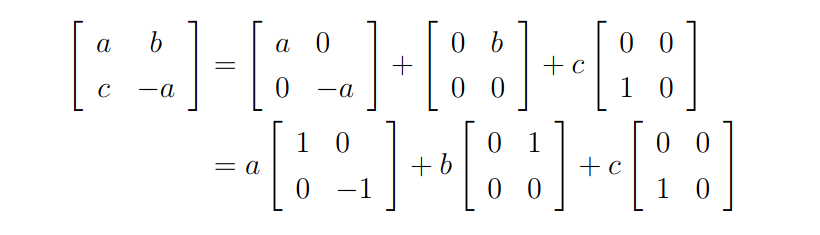
note que conseguimos expressar a matriz geral em termos da combinação linear de três matrizes 2×2 que são linearmente independente. Assim, segue que dim(ker(T)) = 3, logo vamos obter a dimensão da imagem de T via Teorema do Núcleo e da Imagem:
dim(M2×2) = dim(ker(T)) + dim(Im(T)) => dim(Im(T)) = dim(M2×2) – dim(ker(T)) = 4 – 3 = 1.
Assim, do Teorema do Núcleo e da Imagem obtemos que: dim(Im(T)) = 1. Além disso, como dim(ker(T)) é não nula segue que a transformação não é injetiva. Por outro lado, a transformação linear é sobrejetiva uma vez que dim(Im(T)) = 1 que é a mesma dimensão do espaço de saída da transformação linear T.
Referências
- STRANG, Gilbert. Álgebra Linear e suas Aplicações. 4ª ed. São Paulo: Cengage Learning, 2017.
- ANTON, Howard; RORRES, Chris. Introdução à Álgebra Linear. 10ª ed. Porto Alegre: Bookman, 2017.
- LANG, Serge. Álgebra Linear. 3ª ed. Rio de Janeiro: LTC, 2006.
- KOLMAN, Bernard; HILL, David R. Álgebra Linear com Aplicações. 8ª ed. São Paulo: Pearson, 2008.
- LAY, David C. Álgebra Linear e suas Aplicações. Rio de Janeiro: LTC, 2018.
- CHIU, Jiawei; CHUNG, Fan; JOHNSON, John L. A Gentle Introduction to Linear Algebra. Journal of Mathematical Education, New York, v. 45, n. 2, p. 123-136, maio 2020.
- WRIGHT, Stephen. Matrix Computations and Optimization. Journal of Numerical Analysis, Chicago, v. 28, n. 4, p. 567-589, set. 2019.
- BUTTYÁN, Levente; HOLCZER, Tamás. Applications of Linear Algebra in Computer Science. International Journal of Computer Science and Information Security, [S.l.], v. 14, n. 9, p. 35-42, set. 2016.
- Khan Academy. Álgebra Linear. Disponível em: https://pt.khanacademy.org/. Acesso em: 27 set. 2023.
- Math Is Fun. Linear Algebra. Disponível em: https://www.mathsisfun.com/algebra/linear-algebra.html. Acesso em: 27 set. 2023.
- Brilliant. Álgebra Linear. Disponível em: https://brilliant.org/courses/#algebra. Acesso em: 27 set. 2023.





