Teorema do Trabalho-Energia com exercícios para Física 1

O Teorema do Trabalho-Energia é um dos importantes resultados da mecânica clássica que estabelece uma relação direta entre o trabalho produzido em um dado processo com a energia cinética do sistema. Decerto, já nas primeiras disciplinas de física a nível graduação, em particular na Física 1, somos deparados com diversos resultados e problemas interessantes que, por vezes, são desafiadores para nós nesse momento de ingresso em um curso superior de exatas.

Nesse sentido, segue que o Teorema do Trabalho-Energia desempenha um papel muito importante nesse contexto. Pois, é por meio dele que você consegue relacionar o trabalho de um sistema físico com a variação da energia cinética do mesmo. Assim, permitindo que você consiga explorar diversos problemas em física 1 sobre a abordagem da lei da conservação da energia.

Então, tendo isso em vista, nesse artigo nós da MeuGuru traremos para você um texto específico sobre o Teorema do Trabalho-Energia. Com efeito, faremos uma breve discussão sobre o que ele é, sua aplicabilidade e partiremos para sua demonstração e eventual aplicação num exemplo prático que, possivelmente, pode estar em sua prova ou ao menos algum problema bem similar.

Trabalho e Energia na mecânica Newtoniana

Então, com intuito de começarmos a entender um pouco das bases que estabelecem o Teorema do Trabalho-Energia na mecânica newtoniana. Decerto, em toda física, nós procuramos determinar quantidades que sejam conservadas, isto é, que não modificam-se com o tempo. Em verdade, essas quantidades conservadas, por vezes possuem íntima relação com simetrias do sistema as quais foram brilhantemente exploradas por Emmy Noether e hoje estão bem postas sob o Teorema de Noether.

Nesse contexto, emerge que a simetria de invariância temporal nos revela a existência de uma quantidade conservada denominada energia E. Agora, vamos explicar essa frase, quando dizemos que temos invariância temporal, significa dizer que podemos olhar para os problemas de física tanto indo para frente no tempo quanto para trás, de fato, isso é uma consequência da segunda lei de Newton, em particular, de termos uma derivada segunda no tempo que garante essa invariância como mostramos a seguir:

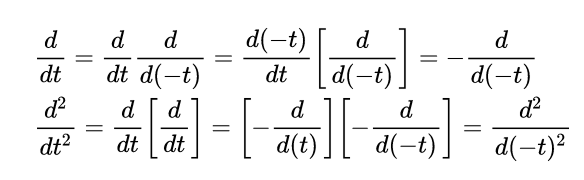
Tal resultado garante que F = ma(t) = ma(-t) e logo o tempo é reversível. Ademais, é consequência disso que temos a lei da conservação da energia, a qual a diz que essa é constante no tempo, ou seja, sua derivada no tempo é igual a zero. Perceba que isso faz bastante sentido, principalmente ao passo que lembramos que a derivada de uma função mede sua taxa de variação com relação ao parâmetro derivado.

Definindo Trabalho

Então, tendo em vista que entendemos a existência dessa lei de conservação, vamos então partir para como podemos definir tanto o conceito de trabalho quanto de energia. Com efeito, definimos o trabalho W de uma força F(x) (em virtude da palavra work do inglês), no contexto da mecânica clássica visto que em diferentes áreas como termodinâmica temos algumas modificações em tal conceito, como sendo a quantidade de energia E que uma partícula deve ter para executar um determinado deslocamento, sendo então, o trabalho W é dado por:

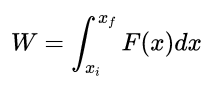
Ademais, perceba que se F(x) for constante, digamos simplesmente que F(x) = F para qualquer valor de x, então a expressão acima fica dada por W = F(x_f – x_i) sendo que os rótulos f e i que aparecem nos x designam as posições finais e iniciais. Aqui é importante ressaltarmos que essa definição pode ser estendida para três dimensões facilmente, entretanto, no contexto de física 1 nos limitamos a uma abordagem com apenas uma dimensão, fazendo assim os desenvolvimentos se resumirem a integrais de uma variável.

Definindo energia potencial e cinética

Por outro lado, além do trabalho é importante definirmos algumas energias, como a energia potencial V(x). Com efeito, essa energia é associada a um campo de forças que age sobre o sistema, basicamente, você pode pensar que ela é a energia que irá guiar o comportamento do corpo/partícula/sistema. Aqui, não nos ateremos muito a essa energia. Entretanto, ela é muito importante e principalmente é valioso que você conheça as expressões para energia potencial gravitacional V(y) = mgy (pois o movimento é na vertical, ou seja, eixo y) e para a energia potencial elástica V_elastica(x) = kx²/2 em que g é a aceleração da gravidade, m é a massa do corpo, k é a constante elástica da mola e x o deslocamento da mola.

Já a energia cinética é aquela que definimos como sendo a energia associada ao movimento do corpo/partícula e/ou sistema. Em geral, se V(x), o potencial, carrega os aspectos físicos sobre como é a trajetória do sistema é a energia cinética que carrega a informação de como ocorre a variação da posição da partícula. Em linhas gerais, a expressão matemática para tal é a seguinte.

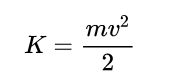
Provando o Teorema do Trabalho-Energia

Agora, feita a devida apresentação das importantes quantidades físicas do trabalho e energia cinética partiremos para o ponto chave do nosso artigo. Então, vamos enunciar o Teorema do Trabalho-Energia cinética, o qual é:

• O Trabalho de uma força de um ponto inicial até um dado ponto final de uma trajetória é igual a variação da energia cinética nos pontos iniciais e finais da trajetória.

Em suma, esse Teorema nos fornece outra forma de computar o trabalho de um corpo que difere do que apresentamos como definição. Tal forma é simplesmente calcular a variação da energia cinética nos pontos iniciais e finais do trajeto. Em verdade, esse resultado pode ser de grande utilidade para você gurunauta, ao passo que várias questões de física 1 trazem tal tema. Particularmente, problemas com relação a conservação da energia ou mesmo de cálculo de trabalho podem, muitas vezes, sequer serem solúveis pelo cálculo da integral do trabalho. Entretanto, conhecendo as velocidades iniciais e finais o problema de calcular o trabalho será apenas uma subtração simples.

Provando o Teorema

Então, posto a discussão acima, iremos agora provar esse Teorema. Para tanto, perceba que partiremos exatamente do que temos: definição de trabalho e segunda lei de Newton. Com efeito, a segunda lei de Newton nos diz que a força resultante de um corpo é F = ma onde a aceleração é: a =dv/dt . Seguindo disso, temos então o seguinte desenvolvimento.

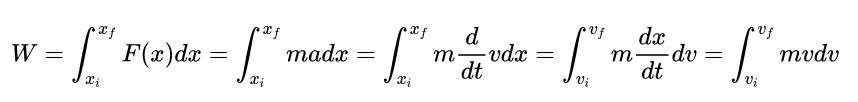
Perceba que nas duas últimas igualdades apenas realizamos uma troca dos diferenciais. Vale a ressalva que esse processo pode ser bem justificado matematicamente, mas isso não é nosso objetivo visto que tal grau de rigor será desnecessário para um curso de física 1. Consequentemente, basta avaliarmos a integral acima que é um processo bem simples de ser feito, veja.

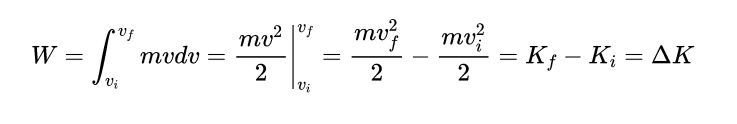
Assim, conseguimos concluir a demosntração do Teorema. Como você pode ver, a prova não envolve nenhuma matemática extraordinária ou exotérica. Na verdade, temos apenas conceitos simples que nós usamos de forma bem inteligente.

Exercício resolvido sobre o Teorema do Trabalho-Energia

Por fim, vamos resolver um problema envolvendo o Teorema do Trabalho-Energia. Com efeito, considere uma pessoa que está num balanço e então um indivíduo empurra tal balanço subitamente com uma dada força F(x). Suponha que o indivíduo inicia o movimento com velocidade igual a 20m/s e tinha massa m = 70kg. Qual o trabalho realizado até chegar no ponto mais alto da trajetória ?.

A solução desse problema é bem simples e envolve conceitos básicos de física. Veja bem, comecemos entendendo que a velocidade inicial é de 20m/s e a velocidade final será zero. Isso segue do fato de que, quando o balanço atinge o ponto mais alto da trajetória sua velocidade será zero e ele inicia o movimento de volta. Ademais, perceba que não precisaremos saber qualquer informação sobre a força F(x) ou sobre como foi a trajetória. Certamente, basta fazermos uso do Teorema de Energia-Trabalho que diz então que o trabalho W será W = 70kg*0/2 – 70*20/2 = -70 * 20 /2= -700 J (joules). E assim, simplesmente temos a resposta do problema, muito simples em gurunauta?

Referências

• NUSSENZVEIG, Herch Moysés. Curso de física básica 1: mecânica. 5. ed. São Paulo: Blucher, 2013. 394 p. ISBN: 9788521207450.
• FEYNMAN, Richard Philips. Física em 12 lições: fáceis e não tão fáceis. 3. ed. Rio de Janeiro: Nova fronteira, 2021. 293 p. ISBN: 9786556401614.
• YOUNG, Hugh D; FREEDMAN, Roger A. , Sears e Zemansky. Física l: mecânica. 14.ed.São Paulo: Pearson, 2016. 430 p. ISBN: 9788543005683.
• HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física, v. 1: mecânica. 10. ed. Rio de Janeiro: LTC, 2018. 366 p. ISBN: 9788521630357.