Nesse artigo vamos falar sobre o Teorema Fundamental do Cálculo (TFC), para que esse Teorema fique totalmente explicado para você.
De fato, no estudo do cálculo diferencial e integral além de perpassamos o estudo de funções, somos apresentados a duas importantes noções: a derivada e a integral. Decerto, as derivadas e integrais constituem boa parte do arcabouço matemático do ensino superior. Nesse âmbito, o importantíssimo Teorema Fundamental do Cálculo ganha sublime destaque. Em verdade, ele permite que as noções de derivadas e integrais sejam relacionadas. Tendo isso em vista, vamos explorar exatamente o que de fato é esse Teorema.
A relação entre derivadas e integrais – TFC
Vamos começar a entender a relação entre derivadas e integrais. Nesse sentido, vamos revisitar, brevemente, as noções que permeiam cada assunto. Todavia, é importante diferenciarmos o sentido algébrico e geométrico das derivadas e integrais. Portanto, vamos revisitar algumas coisas antes de prosseguirmos
Primeiramente, vamos considerar a derivada de uma função f(x), a qual denotamos por
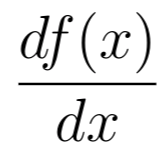
Você deve saber que as derivadas são associadas a reta tangente da curva ponto. Por outro lado, a integral de uma função f(x) é denotada por
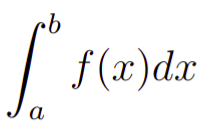
e essa simboliza a área abaixo da curva da função f(x) no intervalo [a,b].
Dado o exposto, você deve ver que parece haver uma relação direta entre áreas e inclinações de retas tangentes. De fato, você está certo, no entanto, é importante vermos essas noções e, também, entendermos que elas são apenas noções geométricas. Nesse sentido, podemos até mesmo dizer que a conexão que há entre a derivada e a integral não é feita através do sentido geométrico, mas, sim, num sentido algébrico. Tendo isso em vista, veremos a seguir como é possível conectar essas noções com o uso do TFC algebricamente.
Teorema Fundamental do Cálculo – parte 1
A primeira parte do Teorema fundamental do cálculo estabelece a conexão efetiva entre derivadas e integrais. Nesse sentido, vamos considerar f(x) uma função e F(x) sua primitiva, isto é

então a parte 1 do TFC nos garante que
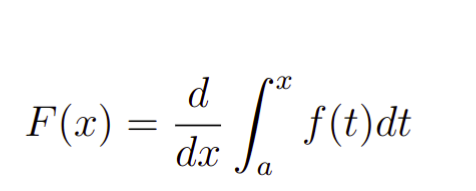
Com isso, temos um resultado incrível. Basicamente, a parte 1 do Teorema nos diz que a aplicação da derivação e integração sucessivamente não modifica a função. Na verdade, ele permite a nós a obtenção de que as operações são “inversas”. Pense nas operações usuais de soma e multiplicação, aqui temos que a derivada é a inversa da integral. Mas lembre-se, isso é feito algebricamente, pois, de fato não faz sentido explorar o sentido geométrico.
Teorema Fundamental do Cálculo – parte 2
A segunda parte do Teorema fundamental do cálculo permite que nós tenhamos uma forma para o cálculo das integrais definidas. De fato, considerando as mesmas funções da seção anteriores teremos que o TFC na parte 2 garantirá que
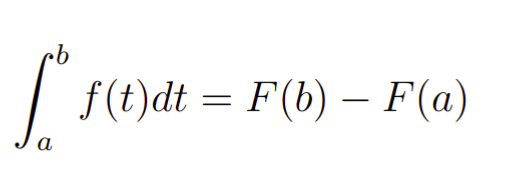
Em suma, esse resultado torna-se imensamente valioso visto que é através dele que iremos efetuar diversos cálculos com integrais. Logo, o problema de calcular uma integral definida passa a ser simplesmente a aplicação dos pontos extremais na função primitiva F.
Fala gurunauta, chegamos ao fim e quero te lembrar para conferir o site da MeuGuru que com toda certeza nós vamos super te ajudar a enfrentar os perrengues do semestre.
