As transformações lineares constituem o coração da Álgebra Linear. Com efeito, o escopo da álgebra linear nos fornece diversas ferramentas robustas que baseiam o desenvolvimento teórico de diversas áreas. Em suma, podemos destacar as seguintes áreas a teoria das equações diferenciais, estudo de sistemas lineares, de espaços de funções e outros.
Todavia, em todo esses assuntos é onipresente as transformações lineares. Ademais, esse é um dos tópicos ainda mais relevantes dentro de um primeiro curso de Álgebra Linear uma vez que as transformações lineares são os objetos matemáticos que desempenham inúmeras aplicações e são de extrema relevância em problemas físicos. Assim, não duvide que dentro desse assunto há uma riqueza de assuntos interessantes como a determinação de autovalores e autoespaços associados, determinação da imagem, núcleo e vários outros aspectos.
Nesse sentido, nós da MeuGuru trouxemos esse texto para você gurunauta. Com efeito, aqui exploraremos as transformações lineares de forma introdutória. Então, a parte 1 da série de artigos sobre transformações lineares versará sobre a determinação das transformações lineares e a verificação da importante propriedade de linearidade que as caracteriza.
O que são transformações lineares ?
Com efeito, as transformações lineares são funções que desempenham um papel central no estudo da álgebra linear. Isto é, elas são responsáveis por mapear vetores de um espaço vetorial para vetores de outro espaço vetorial, preservando a estrutura linear.
Assim, uma transformação linear é caracterizada por duas propriedades fundamentais. Em primeiro lugar, temos a preservação da adição: para quaisquer dois vetores u e v em um espaço vetorial, a transformação linear preserva a adição, ou seja, quando aplicamos a transformação linear à soma dos vetores, obtemos a soma das transformações lineares dos vetores individuais.
Ademais, a segunda propriedade é a preservação da multiplicação por escalar. Para qualquer vetor u em um espaço vetorial e qualquer escalar c, a transformação linear preserva a multiplicação por escalar. Portanto, isso significa que quando aplicamos a transformação linear a um vetor multiplicado por um escalar, obtemos o mesmo resultado que se multiplicássemos a transformação linear do vetor original pelo mesmo escalar. Em resumo, uma transformação é linear se dados os vetores u e v um escalar k for satisfeita a seguinte igualdade:
T(u+kv) = T(u) + k T(v).
Representações
Em verdade, um dos aspectos de grande interesse associado as transformações lineares diz respeito a suas representações. Com efeito, as transformações lineares podem ser representadas por meio de matrizes. De fato, se considerarmos uma base adequada para os espaços vetoriais de partida e chegada, podemos associar uma matriz a uma transformação linear. Assim, essa matriz, chamada de matriz da transformação linear, permite-nos calcular a transformação linear de um vetor através de uma multiplicação de matriz.
Aplicações das transformações lineares
Com efeito, as transformações lineares desempenham um papel crucial em diversas áreas, como geometria, física, ciência da computação e engenharia. Decerto, alguma dessas aplicações inclusive podem ser vistas em alguns dos nossos artigos como: equações diferenciais lineares, transformada de Fourier e a transformada de Laplace.
Dessa forma, elas nos permitem modelar e compreender uma ampla gama de fenômenos e sistemas, além de serem fundamentais para o estudo de sistemas de equações lineares, diagonalização de matrizes, espaços vetoriais e áreas relacionadas da álgebra linear.
Com efeito, a compreensão das transformações lineares é essencial para aprofundar nosso conhecimento sobre a estrutura e propriedades dos espaços vetoriais, bem como para a aplicação prática de conceitos e métodos relacionados à álgebra linear.
Transformações lineares na Mecânica Quântica
Em particular há uma área de aplicações que ganha imenso destaque nesse contexto: a mecânica quântica. Decerto, a Álgebra Linear e as transformações lineares desempenham um papel fundamental na Mecânica Quântica. Com efeito, a Mecânica Quântica, a Álgebra Linear é utilizada para descrever e analisar os estados quânticos e as propriedades dos sistemas quânticos.
Nesse contexto, as transformações lineares são empregadas para representar as mudanças de estado dos sistemas quânticos ao longo do tempo. Com efeito, as transformações lineares na Mecânica Quântica são frequentemente descritas por meio de operadores lineares. Ademais, dizemos que um operador linear na Mecânica Quântica é uma transformação linear que atua sobre os vetores de estado quântico. Esses operadores representam observáveis físicos, como posição, momento e energia, e são fundamentais para o estudo das propriedades e comportamentos dos sistemas quânticos.
Com efeito, as transformações lineares na Mecânica Quântica são responsáveis por descrever a evolução temporal dos estados quânticos. Por meio dessas transformações, podemos determinar como os estados quânticos se modificam ao longo do tempo, permitindo-nos prever e analisar os resultados de medidas e experimentos.
Com efeito, a representação matemática das transformações lineares na Mecânica Quântica é realizada por meio de matrizes ou operadores lineares. Essas matrizes, conhecidas como operadores quânticos, são essenciais para calcular as probabilidades de transição entre estados quânticos, bem como para determinar as propriedades físicas dos sistemas quânticos.
Exemplos resolvidos
Agora, vamos atacar alguns problemas. Uma vez que, agora você já conhece e entende bem o que são as transformações lineares está na hora de vermos na prática como identificamos e verificamos que uma dada transformação é linear. Com efeito, a ideia é simplesmente empregar as condições que chamamos/definimos e que caracterizam a linearidade de modo que possa ser factível verificá-la por desenvolvimento direto.
Nesse sentido, vamos aos exemplos.
Uma transformação linear 3×3
De fato, vamos considerar a seguinte transformação linear e sua matriz associada.
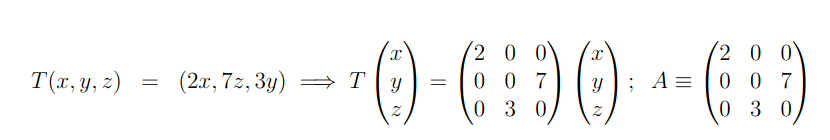
agora, tomemos dois vetores genéricos u = (u1, u2, u3)e v = (v1, v2, v3) e um escalar k de modo que teremos o seguinte desenvolvimento:
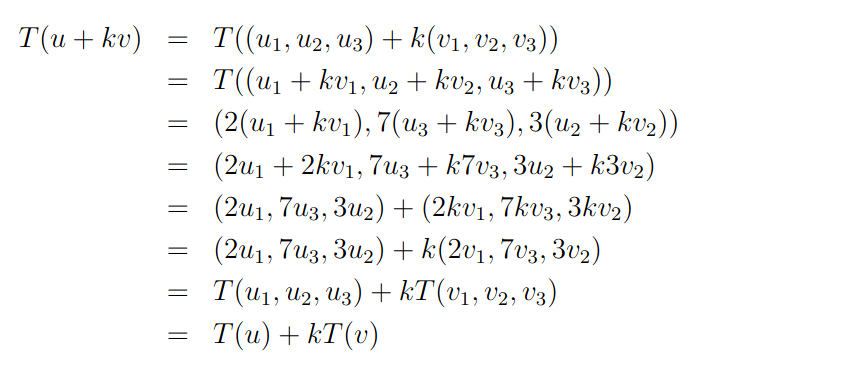
e logo a condição de linearidade é verificada desse modo segue que nossa transformação é linear.
Uma transformação linear de um polinômio
Agora, consideremos a seguinte transformação T que associa elementos do espaço vetorial de polinômios. Com efeito, veja que nesse exemplo não temos uma matriz, todavia, podemos escrever a transformação como uma matriz de modo que teremos o seguinte desenvolvimento.

Então, agora basta prosseguirmos de maneira análoga ao feito anteriormente e verificaremos a linearidade. Com efeito, então teremos o seguinte

Uma transformação não linear !
Agora, vamos ver um contra exemplo. Decerto, não é difícil acharmos exemplos de transformações que não são lineares. Nesse sentido, consideremos a seguinte transformação: T(x,y) = (2x+1,3y). Com efeito, essa não é uma transformação linear, em verdade a propriedade da soma será falha no processo que fazemos acima. Então, veja que teremos o seguinte desenvolvimento para verificarmos que tal transformação é não linear.

Assim, com esse desenvolvimento, verificamos o desejado, isto é, que a transformação é não linear!.
Referências
- STRANG, Gilbert. Álgebra Linear e suas Aplicações. 4ª ed. São Paulo: Cengage Learning, 2017.
- ANTON, Howard; RORRES, Chris. Introdução à Álgebra Linear. 10ª ed. Porto Alegre: Bookman, 2017.
- LANG, Serge. Álgebra Linear. 3ª ed. Rio de Janeiro: LTC, 2006.
- KOLMAN, Bernard; HILL, David R. Álgebra Linear com Aplicações. 8ª ed. São Paulo: Pearson, 2008.
- LAY, David C. Álgebra Linear e suas Aplicações. Rio de Janeiro: LTC, 2018.
- CHIU, Jiawei; CHUNG, Fan; JOHNSON, John L. A Gentle Introduction to Linear Algebra. Journal of Mathematical Education, New York, v. 45, n. 2, p. 123-136, maio 2020.
- WRIGHT, Stephen. Matrix Computations and Optimization. Journal of Numerical Analysis, Chicago, v. 28, n. 4, p. 567-589, set. 2019.
- BUTTYÁN, Levente; HOLCZER, Tamás. Applications of Linear Algebra in Computer Science. International Journal of Computer Science and Information Security, [S.l.], v. 14, n. 9, p. 35-42, set. 2016.
- Khan Academy. Álgebra Linear. Disponível em: https://pt.khanacademy.org/. Acesso em: 27 set. 2023.
- Math Is Fun. Linear Algebra. Disponível em: https://www.mathsisfun.com/algebra/linear-algebra.html. Acesso em: 27 set. 2023.
- Brilliant. Álgebra Linear. Disponível em: https://brilliant.org/courses/#algebra. Acesso em: 27 set. 2023.





